just as the larger war in Europe was breaking out. Although he hoped for a commission as an officer in the army, because he was an academic of Jewish heritage he had to settle for being made a sergeant.43After Einstein formulated his special theory of relativity in 1905, he realized that it was incomplete in at least two ways. First, it held that no physical interaction can propagate faster than the speed of light; that conflicted with Newton’s theory of gravity, which conceived of gravity as a force that acted instantly between distant objects. Second, it applied only to constant-velocity motion. So for the next ten years, Einstein engaged in an interwoven effort to come up with a new field theory of gravity and to generalize his relativity theory so that it applied to accelerated motion.1
His first major conceptual advance had come at the end of 1907, while he was writing about relativity for a science yearbook. As noted earlier, a thought experiment about what a free-falling observer would feel led him to embrace the principle that the local effects of being accelerated and of being in a gravitational field are indistinguishable.* A person in a closed windowless chamber who feels his feet pressed to the floor will not be able to tell whether it’s because the chamber is in outer space being accelerated upward or because it is at rest in a gravitational field. If he pulls a penny from his pocket and lets it go, it will fall to the floor at an accelerating speed in either case. Likewise, a person who feels she is floating in the closed chamber will not know whether it’s because the chamber is in free fall or hovering in a gravity-free region of outer space.2
This led Einstein to the formulation of an “equivalence principle” that would guide his quest for a theory of gravity and his attempt to generalize relativity. “I realized that I would be able to extend or generalize the principle of relativity to apply to accelerated systems in addition to those moving at a uniform velocity,” he later explained. “And in so doing, I expected that I would be able to resolve the problem of gravitation at the same time.”
Just as inertial mass and gravitational mass are equivalent, so too there is an equivalence, he realized, between all inertial effects, such as resistance to acceleration, and gravitational effects, such as weight. His insight was that they are both manifestations of the same structure, which we now sometimes call the inertio-gravitational field.3
One consequence of this equivalence is that gravity, as Einstein had noted, should bend a light beam. That is easy to show using the chamber thought experiment. Imagine that the chamber is being accelerated upward. A laser beam comes in through a pinhole on one wall. By the time it reaches the opposite wall, it’s a little closer to the floor, because the chamber has shot upward. And if you could plot its trajectory across the chamber, it would be curved because of the upward acceleration. The equivalence principle says that this effect should be the same whether the chamber is accelerating upward or is instead resting still in a gravitational field. Thus, light should appear to bend when going through a gravitational field.
For almost four years after positing this principle, Einstein did little with it. Instead, he focused on light quanta. But in 1911, he confessed to Michele Besso that he was weary of worrying about quanta, and he turned his attention back to coming up with a field theory of gravity that would help him generalize relativity. It was a task that would take him almost four more years, culminating in an eruption of genius in November 1915.
In a paper he sent to the Annalen der Physik in June 1911, “On the Influence of Gravity on the Propagation of Light,” he picked up his insight from 1907 and gave it rigorous expression. “In a memoir published four years ago I tried to answer the question whether the propagation of light is influenced by gravitation,” he began. “I now see that one of the most important consequences of my former treatment is capable of being tested experimentally.” After a series of calculations, Einstein came up with a prediction for light passing through the gravitational field next to the sun: “A ray of light going past the sun would undergo a deflection of 0.83 second of arc.”*
Once again, he was deducing a theory from grand principles and postulates, then deriving some predictions that experimenters could proceed to test. As before, he ended his paper by calling for just such a test. “As the stars in the parts of the sky near the sun are visible during total eclipses of the sun, this consequence of the theory may be observed. It would be a most desirable thing if astronomers would take up the question.”4
Erwin Finlay Freundlich, a young astronomer at the Berlin University observatory, read the paper and became excited by the prospect of doing this test. But it could not be performed until an eclipse, when starlight passing near the sun would be visible, and there would be no suitable one for another three years.
So Freundlich proposed that he try to measure the deflection of starlight caused by the gravitational field of Jupiter. Alas, Jupiter did not prove big enough for the task. “If only we had a truly larger planet than Jupiter!” Einstein joked to Freundlich at the end of that summer. “But nature did not deem it her business to make the discovery of her laws easy for us.”5
The theory that light beams could be bent led to some interesting questions. Everyday experience shows that light travels in straight lines. Carpenters now use laser levels to mark off straight lines and construct level houses. If a light beam curves as it passes through regions of changing gravitational fields, how can a straight line be determined?
One solution might be to liken the path of the light beam through a changing gravitational field to that of a line drawn on a sphere or on a surface that is warped. In such cases, the shortest line between two points is curved, a geodesic like a great arc or a great circle route on our globe. Perhaps the bending of light meant that the fabric of space, through which the light beam traveled, was curved by gravity. The shortest path through a region of space that is curved by gravity might seem quite different from the straight lines of Euclidean geometry.
There was another clue that a new form of geometry might be needed. It became apparent to Einstein when he considered the case of a rotating disk. As a disk whirled around, its circumference would be contracted in the direction of its motion when observed from the reference frame of a person not rotating with it. The diameter of the circle, however, would not undergo any contraction. Thus, the ratio of the disk’s circumference to its diameter would no longer be given by pi. Euclidean geometry wouldn’t apply to such cases.
Rotating motion is a form of acceleration, because at every moment a point on the rim is undergoing a change in direction, which means that its velocity (a combination of speed and direction) is undergoing a change. Because non-Euclidean geometry would be necessary to describe this type of acceleration, according to the equivalence principle, it would be needed for gravitation as well.6
Unfortunately, as he had proved at the Zurich Polytechnic, non-Euclidean geometry was not a strong suit for Einstein. Fortunately, he had an old friend and classmate in Zurich for whom it was.
When Einstein moved back to Zurich from Prague in July 1912, one of the first things he did was call on his friend Marcel Grossmann, who had taken the notes Einstein used when he skipped math classes at the Zurich Polytechnic. Einstein had gotten a 4.25 out of 6 in his two geometry courses at the Polytechnic. Grossmann, on the other hand, had scored a perfect 6 in both of his geometry courses, had written his dissertation on non-Euclidean geometry, published seven papers on that topic, and was now the chairman of the math department.7
“Grossmann, you’ve got to help me or I will go crazy,” Einstein said. He explained that he needed a mathematical system that would express—and perhaps even help him discover—the laws that governed the gravitational field. “Instantly, he was all afire,” Einstein recalled of Grossmann’s response.8
Until then, Einstein’s scientific success had been based on his special talent for sniffing out the underlying physical principles of nature. He had left to others the task, which to him seemed less exalted, of finding the best mathematical expressions of those principles, as his Zurich colleague Minkowski had done for special relativity.
But by 1912, Einstein had come to appreciate that math could be a tool for discovering—and not merely describing—nature’s laws. Math was nature’s playbook. “The central idea of general relativity is that gravity arises from the curvature of spacetime,” says physicist James Hartle. “Gravity is geometry.”9
“I am now working exclusively on the gravitation problem and I believe that, with the help of a mathematician friend here, I will overcome all difficulties,” Einstein wrote to the physicist Arnold Sommerfeld. “I have gained enormous respect for mathematics, whose more subtle parts I considered until now, in my ignorance, as pure luxury!”10
Grossmann went home to think about the question. After consulting the literature, he came back to Einstein and recommended the non-Euclidean geometry that had been devised by Bernhard Riemann.11
Riemann (1826–1866) was a child prodigy who invented a perpetual calendar at age 14 as a gift for his parents and went on to study in the great math center of Göttingen, Germany, under Carl Friedrich Gauss, who had been pioneering the geometry of curved surfaces. This was the topic Gauss assigned to Riemann for a thesis, and the result would transform not only geometry but physics.
Euclidean geometry describes flat surfaces. But it does not hold true on curved surfaces. For example, the sum of the angles of a triangle on a flat page is 180°. But look at the globe and picture a triangle formed by the equator as the base, the line of longitude running from the equator to the North Pole through London (longitude 0°) as one side, and the line of longitude running from the equator to the North Pole through New Orleans (longitude 90°) as the third side. If you look at this on a globe, you will see that all three angles of this triangle are right angles, which of course is impossible in the flat world of Euclid.
Gauss and others had developed different types of geometry that could describe the surface of spheres and other curved surfaces. Riemann took things even further: he developed a way to describe a surface no matter how its geometry changed, even if it varied from spherical to flat to hyperbolic from one point to the next. He also went beyond dealing with the curvature of just two-dimensional surfaces and, building on the work of Gauss, explored the various ways that math could describe the curvature of three-dimensional and even four-dimensional space.
That is a challenging concept. We can visualize a curved line or surface, but it is hard to imagine what curved three-dimensional space would be like, much less a curved four dimensions. But for mathematicians, extending the concept of curvature into different dimensions is easy, or at least doable. This involves using the concept of the metric, which specifies how to calculate the distance between two points in space.
On a flat surface with just the normal x and y coordinates, any high school algebra student, with the help of old Pythagoras, can calculate the distance between points. But imagine a flat map (of the world, for example) that represents locations on what is actually a curved globe. Things get stretched out near the poles, and measurement gets more complex. Calculating the actual distance between two points on the map in Greenland is different from doing so for points near the equator. Riemann worked out ways to determine mathematically the distance between points in space no matter how arbitrarily it curved and contorted.12
To do so he used something called a tensor. In Euclidean geometry, a vector is a quantity (such as of velocity or force) that has both a magnitude and a direction and thus needs more than a single simple number to describe it. In non-Euclidean geometry, where space is curved, we need something more generalized—sort of a vector on steroids—in order to incorporate, in a mathematically orderly way, more components. These are called tensors.
A metric tensor is a mathematical tool that tells us how to calculate the distance between points in a given space. For two-dimensional maps, a metric tensor has three components. For three-dimensional space, it has six independent components. And once you get to that glorious four-dimensional entity known as spacetime, the metric tensor needs ten independent components.*
Riemann helped to develop this concept of the metric tensor, which was denoted as gmn and pronounced gee-mu-nu. It had sixteen components, ten of them independent of one another, that could be used to define and describe a distance in curved four-dimensional spacetime.13
The useful thing about Riemann’s tensor, as well as other tensors that Einstein and Grossmann adopted from the Italian mathematicians Gregorio Ricci-Curbastro and Tullio Levi-Civita, is that they are generally covariant. This was an important concept for Einstein as he tried to generalize a theory of relativity. It meant that the relationships between their components remained the same even when there were arbitrary changes or rotations in the space and time coordinate system. In other words, the information encoded in these tensors could go through a variety of transformations based on a changing frame of reference, but the basic laws governing the relationship of the components to each other remained the same.14
Einstein’s goal as he pursued his general theory of relativity was to find the mathematical equations describing two complementary processes:
1. How a gravitational field acts on matter, telling it how to move.
2. And in turn, how matter generates gravitational fields in space-time, telling it how to curve.
His head-snapping insight was that gravity could be defined as the curvature of spacetime, and thus it could be represented by a metric tensor. For more than three years he would fitfully search for the right equations to accomplish his mission.15
Years later, when his younger son, Eduard, asked why he was so famous, Einstein replied by using a simple image to describe his great insight that gravity was the curving of the fabric of spacetime. “When a blind beetle crawls over the surface of a curved branch, it doesn’t notice that the track it has covered is indeed curved,” he said. “I was lucky enough to notice what the beetle didn’t notice.”16
Beginning in that summer of 1912, Einstein struggled to develop gravitational field equations using tensors along the lines developed by Riemann, Ricci, and others. His first round of fitful efforts are preserved in a scratchpad notebook. Over the years, this revealing “Zurich Notebook” has been dissected and analyzed by a team of scholars including Jürgen Renn, John D. Norton, Tilman Sauer, Michel Janssen, and John Stachel.17
In it Einstein pursued a two-fisted approach. On the one hand, he engaged in what was called a “physical strategy,” in which he tried to build the correct equations from a set of requirements dictated by his feel for the physics. At the same time, he pursued a “mathematical strategy,” in which he tried to deduce the correct equations from the more formal math requirements using the tensor analysis that Gross-mann and others recommended.
Einstein’s “physical strategy” began with his mission to generalize the principle of relativity so that it applied to observers who were accelerating or moving in an arbitrary manner. Any gravitational field equation he devised would have to meet the following physical requirements:
• It must revert to Newtonian theory in the special case of weak and static gravitational fields. In other words, under certain normal conditions, his theory would describe Newton’s familiar laws of gravitation and motion.
• It should preserve the laws of classical physics, most notably the conservation of energy and momentum.
• It should satisfy the principle of equivalence, which holds that observations made by an observer who is uniformly accelerating would be equivalent to those made by an observer standing in a comparable gravitational field.
Einstein’s “mathematical strategy,” on the other hand, focused on using generic mathematical knowledge about the metric tensor to find a gravitational field equation that was generally (or at least broadly) covariant.
The process worked both ways: Einstein would examine equations that were abstracted from his physical requirements to check their covariance properties, and he would examine equations that sprang from elegant mathematical formulations to see if they met the requirements of his physics. “On page after page of the notebook, he approached the problem from either side, here writing expressions suggested by the physical requirements of the Newtonian limit and energy-momentum conservation, there writing expressions naturally suggested by the generally covariant quantities supplied by the mathematics of Ricci and Levi-Civita,” says John Norton.18
But something disappointing happened. The two groups of requirements did not mesh. Or at least Einstein thought not. He could not get the results produced by one strategy to meet the requirements of the other strategy.
Using his mathematical strategy, he derived some very elegant equations. At Grossmann’s suggestion, he had begun using a tensor developed by Riemann and then a more suitable one developed by Ricci. Finally, by the end of 1912, he had devised a field equation using a tensor that was, it turned out, pretty close to the one that he would eventually use in his triumphant formulation of late November 1915. In other words, in his Zurich Notebook he had come up with what was quite close to the right solution.19
But then he rejected it, and it would stagnate in his discard pile for more than two years. Why? Among other considerations, he thought (somewhat mistakenly) that this solution did not reduce, in a weak and static field, to Newton’s laws. When he tried it a different way, it did not meet the requirement of the conservation of energy and momentum. And if he introduced a coordinate condition that allowed the equations to satisfy one of these requirements, it proved incompatible with the conditions needed to satisfy the other requirement.20
As a result, Einstein reduced his reliance on the mathematical strategy. It was a decision that he would later regret. Indeed, after he finally returned to the mathematical strategy and it proved spectacularly successful, he would from then on proclaim the virtues—both scientific and philosophical—of mathematical formalism.21
In May 1913, having discarded the equations derived from the mathematical strategy, Einstein and Grossmann produced a sketchy alternative theory based more on the physical strategy. Its equations were constructed to conform to the requirements of energy-momentum conservation and of being compatible with Newton’s laws in a weak static field.
Even though it did not seem that these equations satisfied the goal of being suitably covariant, Einstein and Grossmann felt it was the best they could do for the time being. Their title reflected their tentativeness: “Outline of a Generalized Theory of Relativity and of a Theory of Gravitation.” The paper thus became known as the Entwurf, which was the German word they had used for “outline.”22
For a few months after producing the Entwurf, Einstein was both pleased and depleted. “I finally solved the problem a few weeks ago,” he wrote Elsa. “It is a bold extension of the theory of relativity, together with a theory of gravitation. Now I must give myself some rest, otherwise I will go kaput.”23
However, he was soon questioning what he had wrought. And the more he reflected on the Entwurf, the more he realized that its equations did not satisfy the goal of being generally or even broadly covariant. In other words, the way the equations applied to people in arbitrary accelerated motion might not always be the same.
His confidence in the theory was not strengthened when he sat down with his old friend Michele Besso, who had come to visit him in June 1913, to study the implications of the Entwurf theory. They produced more than fifty pages of notes on their deliberations, each writing about half, which analyzed how the Entwurf accorded with some curious facts that were known about the orbit of Mercury.24
Since the 1840s, scientists had been worrying about a small but unexplained shift in the orbit of Mercury. The perihelion is the spot in a planet’s elliptical orbit when it is closest to the sun, and over the years this spot in Mercury’s orbit had slipped a tiny amount more—about 43 seconds of an arc each century—than what was explained by Newton’s laws. At first it was assumed that some undiscovered planet was tugging at it, similar to the reasoning that had earlier led to the discovery of Neptune. The Frenchman who discovered Mercury’s anomaly even calculated where such a planet would be and named it Vulcan. But it was not there.
Einstein hoped that his new theory of relativity, when its gravitational field equations were applied to the sun, would explain Mercury’s orbit. Unfortunately, after a lot of calculations and corrected mistakes, he and Besso came up with a value of 18 seconds of an arc per century for how far Mercury’s perihelion should stray, which was not even halfway correct. The poor result convinced Einstein not to publish the Mercury calculations. But it did not convince him to discard his Entwurf theory, at least not yet.
Einstein and Besso also looked at whether rotation could be considered a form of relative motion under the equations of the Entwurf theory. In other words, imagine that an observer is rotating and thus experiencing inertia. Is it possible that this is yet another case of relative motion and is indistinguishable from a case where the observer is at rest and the rest of the universe is rotating around him?
The most famous thought experiment along these lines was that described by Newton in the third book of his Principia. Imagine a bucket that begins to rotate as it hangs from a rope. At first the water in the bucket stays rather still and flat. But soon the friction from the bucket causes the water to spin around with it, and it assumes a concave shape. Why? Because inertia causes the spinning water to push outward, and therefore it pushes up the side of the bucket.
Yes, but if we suspect that all motion is relative, we ask: What is the water spinning relative to? Not the bucket, because the water is concave when it is spinning along with the bucket, and also when the bucket stops and the water keeps spinning inside for a while. Perhaps the water is spinning relative to nearby bodies such as the earth that exert gravitational force.
But imagine the bucket spinning in deep space with no gravity and no reference points. Or imagine it spinning alone in an otherwise empty universe. Would there still be inertia? Newton believed so, and said it was because the bucket was spinning relative to absolute space.
When Einstein’s early hero Ernst Mach came along in the mid-nineteenth century, he debunked this notion of absolute space and argued that the inertia existed because the water was spinning relative to the rest of the matter in the universe. Indeed, the same effects would be observed if the bucket was still and the rest of the universe was rotating around it, he said.25
The general theory of relativity, Einstein hoped, would have what he dubbed “Mach’s Principle” as one of its touchstones. Happily, when he analyzed the equations in his Entwurf theory, he concluded that they did seem to predict that the effects would be the same whether a bucket was spinning or was motionless while the rest of the universe spun around it.
Or so Einstein thought. He and Besso made a series of very clever calculations designed to see if indeed this was the case. In their notebook, Einstein wrote a joyous little exclamation at what appeared to be the successful conclusion of these calculations: “Is correct.”
Unfortunately, he and Besso had made some mistakes in this work. Einstein would eventually discover those errors two years later and realize, unhappily, that the Entwurf did not in fact satisfy Mach’s principle. In all likelihood, Besso had already warned him that this might be the case. In a memo that he apparently wrote in August 1913, Besso suggested that a “rotation metric” was not in fact a solution permitted by the field equations in the Entwurf.
But Einstein dismissed these doubts, in letters to Besso as well as to Mach and others, at least for the time being.26 If experiments upheld the theory, “your brilliant investigations on the foundations of mechanics will have received a splendid confirmation,” Einstein wrote to Mach days after the Entwurf was published. “For it shows that inertia has its origin in some kind of interaction of the bodies, exactly in accordance with your argument about Newton’s bucket experiment.”27
What worried Einstein most about the Entwurf, justifiably, was that its mathematical equations did not prove to be generally covariant, thus deflating his goal of assuring that the laws of nature were the same for an observer in accelerated or arbitrary motion as they were for an observer moving at a constant velocity. “Regrettably, the whole business is still so very tricky that my confidence in the theory is still rather hesitant,” he wrote in reply to a warm letter of congratulations from Lorentz.“The gravitational equations themselves unfortunately do not have the property of general covariance.”28
He was soon able to convince himself, at least for a while, that this was inevitable. In part he did so through a thought experiment, which became known as the “hole argument,”29 that seemed to suggest that the holy grail of making the gravitational field equations generally covariant was impossible to reach, or at least physically uninteresting. “The fact that the gravitational equations are not generally covariant, something that quite disturbed me for a while, is unavoidable,” he wrote a friend. “It can easily be shown that a theory with generally covariant equations cannot exist if the demand is made that the field is mathematically completely determined by matter.”30
For the time being, very few physicists embraced Einstein’s new theory, and many came forth to denounce it.31 Einstein professed pleasure that the issue of relativity “has at least been taken up with the requisite vigor,” as he put it to his friend Zangger. “I enjoy controversies. In the manner of Figaro: ‘Would my noble Lord venture a little dance? He should tell me! I will strike up the tune for him.’ ”32
Through it all, Einstein continued to try to salvage his Entwurf approach. He was able to find ways, or so he thought, to achieve enough covariance to satisfy most aspects of his principle about the equivalence of gravity and acceleration. “I succeeded in proving that the gravitational equations hold for arbitrarily moving reference systems, and thus that the hypothesis of the equivalence of acceleration and gravitational field is absolutely correct,” he wrote Zangger in early 1914. “Nature shows us only the tail of the lion. But I have no doubt that the lion belongs with it even if he cannot reveal himself all at once. We see him only the way a louse that sits upon him would.”33
There was, Einstein knew, one way to quell doubts. He often concluded his papers with suggestions for how future experiments could confirm whatever he had just propounded. In the case of general relativity, this process had begun in 1911, when he specified with some precision how much he thought light from a star would be deflected by the gravity of the sun.
This was something that could, he hoped, be measured by photographing stars whose light passed close to the sun and determining whether there appeared to be a tiny shift in their position compared to when their light did not have to pass right by the sun. But this was an experiment that had to be done during an eclipse, when the starlight would be visible.
So it was not surprising that, with his theory arousing noisy attacks from colleagues and quiet doubts in his own mind, Einstein became keenly interested in what could be discovered during the next suitable total eclipse of the sun, which was due to occur on August 21, 1914. That would require an expedition to the Crimea, in Russia, where the path of the eclipse would fall.
Einstein was so eager to have his theory tested during the eclipse that, when it seemed there might be no money for such an expedition, he offered to pay part of the costs himself. Erwin Freundlich, the young Berlin astronomer who had read the light-bending predictions in Einstein’s 1911 paper and become eager to prove him correct, was ready to take the lead. “I am extremely pleased that you have taken up the question of the bending of light with so much zeal,” Einstein wrote him in early 1912. In August 1913, he was still bombarding the astronomer with encouragement.“Nothing more can be done by the theorists,” he wrote. “In this matter it is only you, the astronomers, who can next year perform a simply invaluable service to theoretical physics.”34
Freundlich got married in August 1913 and decided to take his honeymoon in the mountains near Zurich, in the hope that he could meet Einstein. It worked. When Freundlich described his honeymoon schedule in a letter, Einstein invited him over for a visit. “This is wonderful because it fits in with our plans,” Freundlich wrote his fiancée, whose reaction to the prospect of spending part of her honeymoon with a theoretical physicist she had never met is lost to history.
When the newlyweds pulled into the Zurich train station, there was a disheveled Einstein wearing, as Freundlich’s wife recalled, a large straw hat, with the plump chemist Fritz Haber at his side. Einstein brought the group to a nearby town where he was giving a lecture, after which he took them to lunch. Not surprisingly, he had forgotten to bring any money, and an assistant who had come along slipped him a 100 franc note under the table. For most of the day, Freundlich discussed gravity and the bending of light with Einstein, even when the group went on a nature hike, leaving his new wife to admire the scenery in peace.35
At his speech that day, which was on general relativity, Einstein pointed out Freundlich to the audience and called him “the man who will be testing the theory next year.”The problem, however, was raising the money. At the time, Planck and others were trying to lure Einstein from Zurich to Berlin to become a member of the Prussian Academy, and Einstein used the courtship to write Planck and urge him to provide Freundlich the money to undertake the task.
In fact, on the very day that Einstein formally accepted the Berlin post and election to the Academy—December 7, 1913—he wrote Freundlich with the offer to reach into his own pocket. “If the Academy shies away from it, then we will get that little bit of mammon from private individuals,” said Einstein. “Should everything fail, then I will pay for the thing myself out of the little bit that I have saved, at least the first 2,000 marks.” The main thing, Einstein stressed, was that Freundlich should proceed with his preparations. “Just go ahead and order the photographic plates, and do not let the time be squandered because of the money problem.”36
As it turned out, there were enough private donations, mainly from the Krupp Foundation, to make the expedition possible. “You can imagine how happy I am that the external difficulties of your undertaking have now more or less been overcome,” Einstein wrote. He added a note of confidence about what would be found: “I have considered the theory from every angle, and I have every confidence in the thing.”37
Freundlich and two colleagues left Berlin on July 19 for the Crimea, where they were joined by a group from the Córdoba observatory in Argentina. If all went well, they would have two minutes to make photographs that could be used to analyze whether the starlight was deflected by the sun’s gravity.
All did not go well. Twenty days before the eclipse, Europe tumbled into World War I and Germany declared war on Russia. Freundlich and his German colleagues were captured by the Russian army, and their equipment was confiscated. Not surprisingly, they were unable to convince the Russian soldiers that, with all of their powerful cameras and location devices, they were mere astronomers planning to gaze at the stars in order to better understand the secrets of the universe.
Even if they had been granted safe passage, it is likely that the observations would have failed. The skies were cloudy during the minutes of the eclipse, and an American group that was also in the region was unable to get any usable photographs.38
Yet the termination of the eclipse mission had a silver lining. Einstein’s Entwurf equations were not correct. The degree to which gravity would deflect light, according to Einstein’s theory at the time, was the same as that predicted by Newton’s emission theory of light. But, as Einstein would discover a year later, the correct prediction would end up being twice that. If Freundlich had succeeded in 1914, Einstein might have been publicly proven wrong.
“My good old astronomer Freundlich, instead of experiencing a solar eclipse in Russia, will now be experiencing captivity there,” Einstein wrote to his friend Ehrenfest. “I am concerned about him.”39There was no need to worry. The young astronomer was released in a prisoner exchange within weeks.
Einstein, however, had other reasons to worry in August 1914. His marriage had just exploded. His masterpiece theory still needed work. And now his native country’s nationalism and militarism, traits that he had abhorred since childhood, had plunged it into a war that would cast him as a stranger in a strange land. In Germany, it would turn out, that was a dangerous position to be in.
The chain reaction that pushed Europe into war in August 1914 inflamed the patriotic pride of the Prussians and, in an equal and opposite reaction, the visceral pacifism of Einstein, a man so gentle and averse to conflict that he even disliked playing chess. “Europe in its madness has now embarked on something incredibly preposterous,” he wrote Ehrenfest that month. “At such times one sees to what deplorable breed of brutes we belong.”40
Ever since he ran away from Germany as a schoolboy and was exposed to the gauzy internationalism of Jost Winteler in Aarau, Einstein had harbored sentiments that disposed him toward pacifism, one-world federalism, and socialism. But he had generally shunned public activism.
World War I changed that. Einstein would never forsake physics, but he would henceforth be unabashedly public, for most of his life, in pushing his political and social ideals.
The irrationality of the war made Einstein believe that scientists in fact had a special duty to engage in public affairs. “We scientists in particular must foster internationalism,” he said. “Unfortunately, we have had to suffer serious disappointments even among scientists in this regard.”41 He was especially appalled by the lockstep pro-war mentality of his three closest colleagues, the scientists who had lured him to Berlin: Fritz Haber, Walther Nernst, and Max Planck.42
Haber was a short, bald, and dapper chemist who was born Jewish but tried mightily to assimilate by converting, getting baptized, and adopting the dress, manner, and even pince-nez glasses of a proper Prussian. The director of the chemistry institute where Einstein had his office, he had been mediating the war between Einstein and Mari just as the larger war in Europe was breaking out. Although he hoped for a commission as an officer in the army, because he was an academic of Jewish heritage he had to settle for being made a sergeant.43
Haber reorganized his institute to develop chemical weapons for Germany. He had already found a way to synthesize ammonia from nitrogen, which permitted the Germans to mass-produce explosives. He then turned his attention to making deadly chlorine gas, which, heavier than air, would flow down into the trenches and painfully asphyxiate soldiers by burning through their throats and lungs. In April 1915, modern chemical warfare was inaugurated when some five thousand French and Belgians met that deadly fate at Ypres, with Haber personally supervising the attack. (In an irony that may have been lost on the inventor of dynamite, who endowed the prize, Haber won the 1918 Nobel in chemistry for his process of synthesizing ammonia.)
His colleague and occasional academic rival Nernst, bespectacled and 50, had his wife inspect his style as he practiced marching and saluting in front of their house. Then he took his private car and showed up at the western front to be a volunteer driver. Upon his return to Berlin, he experimented with tear gas and other irritants that could be used as a humane way to flush the enemy out of the trenches, but the generals decided they preferred the lethal approach that Haber was taking, so Nernst became part of that effort.
Even the revered Planck supported what he called Germany’s “just war.” As he told his students when they went off to battle, “Germany has drawn its sword against the breeding ground of insidious perfidy.”44
Einstein was able to avoid letting the war cause a personal rift between him and his three colleagues, and he spent the spring of 1915 tutoring Haber’s son in math.45 But when they signed a petition defending Germany’s militarism, he felt compelled to break with them politically.
The petition, published in October 1914, was titled “Appeal to the Cultured World” and became known as the “Manifesto of the 93,” after the number of intellectuals who endorsed it. With scant regard for the truth, it denied that the German army had committed any attacks on civilians in Belgium and went on to proclaim that the war was necessary. “Were it not for German militarism, German culture would have been wiped off the face of the earth,” it asserted. “We shall wage this fight to the very end as a cultured nation, a nation that holds the legacy of Goethe, Beethoven, and Kant no less sacred than hearth and home.”46
It was no surprise that among the scientists who signed was the conservative Philipp Lenard, of photoelectric effect fame, who would later become a rabid anti-Semite and Einstein hater. What was distressing was that Haber, Nernst, and Planck also signed. As both citizens and scientists, they had a natural instinct to go along with the sentiments of others. Einstein, on the other hand, often displayed a natural inclination not to go along, which sometimes was an advantage both as a scientist and as a citizen.
A charismatic adventurer and occasional physician named Georg Friedrich Nicolai, who had been born Jewish (his original name was Lewinstein) and was a friend of both Elsa and her daughter Ilse, worked with Einstein to write a pacifist response. Their “Manifesto to Europeans” appealed for a culture that transcended nationalism and attacked the authors of the original manifesto. “They have spoken in a hostile spirit,” Einstein and Nicolai wrote. “Nationalist passions cannot excuse this attitude, which is unworthy of what the world has heretofore called culture.”
Einstein suggested to Nicolai that Max Planck, even though he had been one of the signers of the original manifesto, might also want to participate in their countermanifesto because of his “broad-mindedness and good will.” He also gave Zangger’s name as a possibility. But neither man, apparently, was willing to get involved. In an indication of the temper of the times, Einstein and Nicolai were able to garner only two other supporters. So they dropped their effort, and it was not published at the time.47
Einstein also became an early member of the liberal and cautiously pacifist New Fatherland League, a club that pushed for an early peace and the establishment of a federal structure in Europe to avoid future conflicts. It published a pamphlet titled “The Creation of the United States of Europe,” and it helped get pacifist literature into prisons and other places. Elsa went with Einstein to some of the Monday evening meetings until the group was banned in early 1916.48
One of the most prominent pacifists during the war was the French writer Romain Rolland, who had tried to promote friendship between his country and Germany. Einstein visited him in September 1915 near Lake Geneva. Rolland noted in his diary that Einstein, speaking French laboriously, gave “an amusing twist to the most serious of subjects.”
As they sat on a hotel terrace amid swarms of bees plundering the flowering vines, Einstein joked about the faculty meetings in Berlin where each of the professors would anguish over the topic “why are we Germans hated in the world” and then would “carefully steer clear of the truth.” Daringly, maybe even recklessly, Einstein openly said that he thought Germany could not be reformed and therefore hoped the allies would win, “which would smash the power of Prussia and the dynasty.”49
The following month, Einstein got into a bitter exchange with Paul Hertz, a noted mathematician in Göttingen who was, or had been, a friend. Hertz was an associate member of the New Fatherland League with Einstein, but he had shied away from becoming a full member when it became controversial. “This type of cautiousness, not standing up for one’s rights, is the cause of the entire wretched political situation,” Einstein berated. “You have that type of valiant mentality the ruling powers love so much in Germans.”
“Had you devoted as much care to understanding people as to understanding science, you would not have written me an insulting letter,” Hertz replied. It was a telling point, and true. Einstein was better at fathoming physical equations than personal ones, as his family knew, and he admitted so in his apology. “You must forgive me, particularly since—as you yourself rightly say—I have not bestowed the same care to understanding people as to understanding science,” he wrote.50
In November, Einstein published a three-page essay titled “My Opinion of the War” that skirted the border of what was permissible, even for a great scientist, to say in Germany. He speculated that there existed “a biologically determined feature of the male character” that was one of the causes of wars. When the article was published by the Goethe League that month, a few passages were deleted for safety’s sake, including an attack on patriotism as potentially containing “the moral requisites of bestial hatred and mass murder.”51
The idea that war had a biological basis in male aggression was a topic Einstein also explored in a letter to his friend in Zurich, Heinrich Zangger. “What drives people to kill and maim each other so savagely?” Einstein asked. “I think it is the sexual character of the male that leads to such wild explosions.”
The only method of containing such aggression, he argued, was a world organization that had the power to police member nations.52 It was a theme he would pick up again eighteen years later, in the final throes of his pure pacifism, when he engaged in a public exchange of letters with Sigmund Freud on both male psychology and the need for world government.
The early months of the war in 1915 made Einstein’s separation from Hans Albert and Eduard more difficult, both emotionally and logistically. They wanted him to come visit them in Zurich for Easter that year, and Hans Albert, who was just turning 11, wrote him two letters designed to pull at his heart: “I just think: At Easter you’re going to be here and we’ll have a Papa again.”
In his next postcard, he said that his younger brother told him about having a dream “that Papa was here.” He also described how well he was doing in math. “Mama assigns me problems; we have a little booklet; I could do the same with you as well.”53
The war made it impossible for him to come at Easter, but he responded to the postcards by promising Hans Albert that he would come in July for a hiking vacation in the Swiss Alps. “In the summer I will take a trip with just you alone for a fortnight or three weeks,” he wrote. “This will happen every year, and Tete [Eduard] may also come along when he is old enough for it.”
Einstein also expressed his delight that his son had taken a liking to geometry. It had been his “favorite pastime” when he was about the same age, he said, “but I had no one to demonstrate anything to me, so I had to learn it from books.” He wanted to be with his son to help teach him math and “tell you many fine and interesting things about science and much else.” But that would not always be possible. Perhaps they could do it by mail? “If you write me each time what you already know, I’ll give you a nice little problem to solve.” He sent along a toy for each of his sons, along with an admonition to brush their teeth well. “I do the same and am very happy now to have kept enough healthy teeth.”54
But the tension in the family worsened. Einstein and Mari exchanged letters arguing about both money and vacation timing, and at the end of June a curt postcard came from Hans Albert. “If you’re so unfriendly to her,” he said of his mother, “I don’t want to go with you.” So Einstein canceled his planned trip to Zurich and instead went with Elsa and her two daughters to the Baltic sea resort of Sellin.
Einstein was convinced that Mari was turning the children against him. He suspected, probably correctly, that her hand was behind the postcards Hans Albert was sending, both the plaintive ones making him feel guilty for not being in Zurich and the sharper ones rejecting vacation hikes. “My fine boy had been alienated from me for a few years already by my wife, who has a vengeful disposition,” he complained to Zangger. “The postcard I received from little Albert had been inspired, if not downright dictated, by her.”
He asked Zangger, who was a professor of medicine, to check on young Eduard, who had been suffering ear infections and other ailments. “Please write me what is wrong with my little boy,” he pleaded. “I’m particularly fondly attached to him; he was still so sweet to me and innocent.”55
It was not until the beginning of September that he finally made it to Switzerland. Mari felt it would be proper for him to stay with her and the boys, despite the strain. They were, after all, still married. She had hopes of reconciling. But Einstein showed no interest in being with her. Instead, he stayed in a hotel and spent a lot of time with his friends Michele Besso and Heinrich Zangger.
As it turned out, he got a chance to see his sons only twice during the entire three weeks he was in Switzerland. In a letter to Elsa, he blamed his estranged wife: “The cause was mother’s fear of the little ones becoming too dependent on me.” Hans Albert let his father know that the whole visit made him feel uncomfortable.56
After Einstein returned to Berlin, Hans Albert paid a call on Zangger. The kindly medical professor, friends of all sides in the dispute, tried to work out an accord so that Einstein could visit his sons. Besso also played intermediary. Einstein could see his sons, Besso advised in a formal letter he wrote after consulting with Mari, but not in Berlin nor in the presence of Elsa’s family. It would be best to do it at “a good Swiss inn,” initially just with Hans Albert, where they could spend some time on their own free of all distractions. Over Christmas, Hans Albert was planning to visit Besso’s family, and he suggested that perhaps Einstein could come then.57
What made the flurry of political and personal turmoil in the fall of 1915 so remarkable was that it highlighted Einstein’s ability to concentrate on, and compartmentalize, his scientific endeavors despite all distractions. During that period, with great effort and anxiety, he was engaged in a competitive rush to what he later called the greatest accomplishment of his life.58
Back when Einstein had moved to Berlin in the spring of 1914, his colleagues had assumed that he would set up an institute and attract acolytes to work on the most pressing problem in physics: the implications of quantum theory. But Einstein was more of a lone wolf. Unlike Planck, he did not want a coterie of collaborators or protégés, and he preferred to focus on what again had become his personal passion: the generalization of his theory of relativity.59
So after his wife and sons left him for Zurich, Einstein moved out of their old apartment and rented one that was nearer to Elsa and the center of Berlin. It was a sparsely furnished bachelor’s refuge, but still rather spacious: it had seven rooms on the third floor of a new five-story building.60
Einstein’s study at home featured a large wooden writing table that was cluttered with piles of papers and journals. Padding around this hermitage, eating and working at whatever hours suited him, sleeping when he had to, he waged his solitary struggle.
Through the spring and summer of 1915, Einstein wrestled with his Entwurf theory, refining it and defending it against a variety of challenges. He began calling it “the general theory” rather than merely “a generalized theory” of relativity, but that did not mask its problems, which he kept trying to deflect.
He claimed that his equations had the greatest amount of covariance that was permissible given his hole argument and other strictures of physics, but he began to suspect that this was not correct. He also got into an exhausting debate with the Italian mathematician Tullio Levi-Civita, who pointed out problems with his handling of the tensor calculus. And there was still the puzzle of the incorrect result the theory gave for the shift in Mercury’s orbit.
At least his Entwurf theory still successfully explained—or so he thought through the summer of 1915—rotation as being a form of relative motion, that is, a motion that could be defined only relative to the positions and motions of other objects. His field equations, he thought, were invariant under the transformation to rotating coordinates.61
Einstein was confident enough in his theory to show it off at a weeklong series of two-hour lectures, starting at the end of June 1915, at the University of Göttingen, which had become the preeminent center for the mathematical side of theoretical physics. Foremost among the geniuses there was David Hilbert, and Einstein was particularly eager—too eager, it would turn out—to explain all the intricacies of relativity to him.
The visit to Göttingen was a triumph. Einstein exulted to Zangger that he had “the pleasurable experience of convincing the mathematicians there thoroughly.” Of Hilbert, a fellow pacifist, he added, “I met him and became quite fond of him.” A few weeks later, after again reporting, “I was able to convince Hilbert of the general theory of relativity,” Einstein called him “a man of astonishing energy and independence.” In a letter to another physicist, Einstein was even more effusive: “In Göttingen I had the great pleasure of seeing that everything was understood down to the details. I am quite enchanted with Hilbert!”62
Hilbert was likewise enchanted with Einstein and his theory. So much so that he soon set out to see if he could beat Einstein to the goal of getting the field equations right. Within three months of his Göttingen lectures, Einstein was confronted with two distressing discoveries: that his Entwurf theory was indeed flawed, and that Hilbert was racing feverishly to come up with the correct formulations on his own.
Einstein’s realization that his Entwurf theory was unraveling came from an accumulation of problems. But it culminated with two major blows in early October 1915.
The first was that, upon rechecking, Einstein found that the Entwurf equations did not actually account for rotation as he had thought.63 He hoped to prove that rotation could be conceived of as just another form of relative motion, but it turned out that the Entwurf didn’t actually prove this. The Entwurf equations were not, as he had believed, covariant under a transformation that uniformly rotated the coordinate axes.
Besso had warned him in a memo in 1913 that this seemed to be a problem. But Einstein had ignored him. Now, upon redoing his calculations, he was dismayed to see this pillar knocked away. “This is a blatant contradiction,” he lamented to the astronomer Freundlich.
He assumed that the same mistake also accounted for his theory’s inability to account fully for the shift in Mercury’s orbit. And he despaired that he would not be able to find the problem. “I do not believe I am able to find the mistake myself, for in this matter my mind is too set in a deep rut.”64
In addition, he realized that he had made a mistake in what was called his “uniqueness” argument: that the sets of conditions required by energy-momentum conservation and other physical restrictions uniquely led to the field equations in the Entwurf. He wrote Lorentz explaining in detail his previous “erroneous assertions.”65
Added to these problems were ones he already knew about: the Entwurf equations were not generally covariant, meaning that they did not really make all forms of accelerated and nonuniform motion relative, and they did not fully explain Mercury’s anomalous orbit. And now, as this edifice was crumbling, he could hear what seemed to be Hilbert’s footsteps gaining on him from Göttingen.
Part of Einstein’s genius was his tenacity. He could cling to a set of ideas, even in the face of “apparent contradiction” (as he put it in his 1905 relativity paper). He also had a deep faith in his intuitive feel for the physical world. Working in a more solitary manner than most other scientists, he held true to his own instincts, despite the qualms of others.
But although he was tenacious, he was not mindlessly stubborn. When he finally decided his Entwurf approach was untenable, he was willing to abandon it abruptly. That is what he did in October 1915.
To replace his doomed Entwurf theory, Einstein shifted his focus from the physical strategy, which emphasized his feel for basic principles of physics, and returned to a greater reliance on a mathematical strategy, which made use of the Riemann and Ricci tensors. It was an approach he had used in his Zurich notebooks and then abandoned, but on returning to it he found that it could provide a way to generate generally covariant gravitational field equations. “Einstein’s reversal,” writes John Norton, “parted the waters and led him from bondage into the promised land of general relativity.”66
Of course, as always, his approach remained a mix of both strategies. To pursue a revitalized mathematical strategy, he had to revise the physical postulates that were the foundation for his Entwurf theory. “This was exactly the sort of convergence of physical and mathematical considerations that eluded Einstein in the Zurich notebook and in his work on the Entwurf theory,” write Michel Janssen and Jürgen Renn.67
Thus he returned to the tensor analysis that he had used in Zurich, with its greater emphasis on the mathematical goal of finding equations that were generally covariant. “Once every last bit of confidence in the earlier theories had given way,” he told a friend, “I saw clearly that it was only through general covariance theory, i.e., with Riemann’s covariant, that a satisfactory solution could be found.”68
The result was an exhausting, four-week frenzy during which Einstein wrestled with a succession of tensors, equations, corrections, and updates that he rushed to the Prussian Academy in a flurry of four Thursday lectures. It climaxed, with the triumphant revision of Newton’s universe, at the end of November 1915.
Every week, the fifty or so members of the Prussian Academy gathered in the grand hall of the Prussian State Library in the heart of Berlin to address each other as “Your Excellency” and listen to fellow members pour forth their wisdom. Einstein’s series of four lectures had been scheduled weeks earlier, but until they began—and even after they had begun—he was still working furiously on his revised theory.
The first was delivered on November 4. “For the last four years,” he began, “I have tried to establish a general theory of relativity on the assumption of the relativity even of non-uniform motion.” Referring to his discarded Entwurf theory, he said he “actually believed I had discovered the only law of gravitation” that conformed to physical realities.
But then, with great candor, he detailed all of the problems that theory had encountered. “For that reason, I completely lost trust in the field equations” that he had been defending for more than two years. Instead, he said, he had now returned to the approach that he and his mathematical caddy, Marcel Grossmann, had been using in 1912. “Thus I went back to the requirement of a more general covariance of the field equations, which I had left only with a heavy heart when I worked together with my friend Grossmann. In fact, we had then already come quite close to the solution.”
Einstein reached back to the Riemann and Ricci tensors that Grossmann had introduced him to in 1912. “Hardly anyone who truly understands it can resist the charm of this theory,” he lectured. “It signifies a real triumph of the method of the calculus founded by Gauss, Riemann, Christoffel, Ricci, and Levi-Civita.”69
This method got him much closer to the correct solution, but his equations on November 4 were still not generally covariant. That would take another three weeks.
Einstein was in the throes of one of the most concentrated frenzies of scientific creativity in history. He was working, he said, “horrendously intensely.”70 In the midst of this ordeal, he was also still dealing with the personal crisis within his family. Letters arrived from both his wife and Michele Besso, who was acting on her behalf, that pressed the issue of his financial obligations and discussed the guidelines for his contact with his sons.
On the very day he turned in his first paper, November 4, he wrote an anguished—and painfully poignant—letter to Hans Albert, who was in Switzerland:
I will try to be with you for a month every year so that you will have a father who is close to you and can love you. You can learn a lot of good things from me that no one else can offer you. The things I have gained from so much strenuous work should be of value not only to strangers but especially to my own boys. In the last few days I completed one of the finest papers of my life. When you are older, I will tell you about it.
He ended with a small apology for seeming so distracted: “I am often so engrossed in my work that I forget to eat lunch.”71
Einstein also took time off from furiously revising his equations to engage in an awkward fandango with his erstwhile friend and competitor David Hilbert, who was racing him to find the equations of general relativity. Einstein had been informed that the Göttingen mathematician had figured out the flaws in the Entwurf equations. Worried about being scooped, he wrote Hilbert a letter saying that he himself had discovered the flaws four weeks earlier, and he sent along a copy of his November 4 lecture. “I am curious whether you will take kindly to this new solution,” Einstein asked with a touch of defensiveness.72
Hilbert was not only a better pure mathematician than Einstein, he also had the advantage of not being as good a physicist. He did not get all wrapped up, the way Einstein did, in making sure that any new theory conformed to Newton’s old one in a weak static field or that it obeyed the laws of causality. Instead of a dual math-and-physics strategy, Hilbert pursued mainly a math strategy, focusing on finding the equations that were covariant. “Hilbert liked to joke that physics was too complicated to be left to the physicists,” notes Dennis Overbye.73
Einstein presented his second paper the following Thursday, November 11. In it, he used the Ricci tensor and imposed new coordinate conditions that allowed the equations thus to be generally covariant. As it turned out, that did not greatly improve matters. Einstein was still close to the final answer, but making little headway.74
Once again, he sent the paper off to Hilbert. “If my present modification (which does not change the equations) is legitimate, then gravitation must play a fundamental role in the composition of matter,” Einstein said. “My own curiosity is interfering with my work!”75
The reply that Hilbert sent the next day must have unnerved Einstein. He said he was about ready to oblige with “an axiomatic solution to your great problem.” He had planned to hold off discussing it until he explored the physical ramifications further. “But since you are so interested, I would like to lay out my theory in very complete detail this coming Tuesday,” which was November 16.
He invited Einstein to come to Göttingen and have the dubious pleasure of personally hearing him lay out the answer. The meeting would begin at 6 p.m., and Hilbert helpfully provided Einstein with the arrival times of the two afternoon trains from Berlin. “My wife and I would be very pleased if you stayed with us.”
Then, after signing his name, Hilbert felt compelled to add what must surely have been a tantalizing and disconcerting postscript. “As far as I understand your new paper, the solution given by you is entirely different from mine.”
Einstein wrote four letters on November 15, a Monday, that give a glimpse into why he was suffering stomach pains. To his son Hans Albert, he suggested that he would like to travel to Switzerland around Christmas and New Year’s to visit him. “Maybe it would be better if we were alone somewhere,” such as at a secluded inn, he suggested to his son. “What do you think?”
He also wrote his estranged wife a conciliatory letter that thanked her for her willingness not “to undermine my relations with the boys.” And he reported to their mutual friend Zangger, “I have modified the theory of gravity, having realized that my earlier proofs had a gap ...I shall be glad to come to Switzerland at the turn of the year in order to see my dear boy.”76
Finally, he replied to Hilbert and declined his invitation to visit Göttingen the next day. His letter did not hide his anxiety: “Your analysis interests me tremendously . . . The hints you gave in your messages awaken the greatest of expectations. Nevertheless, I must refrain from traveling to Göttingen for the moment ...I am tired out and plagued by stomach pains . . . If possible, please send me a correction proof of your study to mitigate my impatience.”77
Fortunately for Einstein, his anxiety was partly alleviated that week by a joyous discovery. Even though he knew his equations were not in final form, he decided to see whether the new approach he was taking would yield the correct results for what was known about the shift in Mercury’s orbit. Because he and Besso had done the calculations once before (and gotten a disappointing result), it did not take him long to redo the calculations using his revised theory.
The answer, which he triumphantly announced in the third of his four November lectures, came out right: 43 arc-seconds per century.78 “This discovery was, I believe, by far the strongest emotional experience in Einstein’s scientific life, perhaps in all his life,” Abraham Pais later said. He was so thrilled he had heart palpitations, as if “something had snapped” inside. “I was beside myself with joyous excitement,” he told Ehrenfest. To another physicist he exulted: “The results of Mercury’s perihelion movement fills me with great satisfaction. How helpful to us is astronomy’s pedantic accuracy, which I used to secretly ridicule!”79
In the same lecture, he also reported on another calculation he had made. When he first began formulating general relativity eight years earlier, he had said that one implication was that gravity would bend light. He had previously figured that the bending of light by the gravitational field next to the sun would be approximately 0.83 arc-second, which corresponded to what would be predicted by Newton’s theory when light was treated as if a particle. But now, using his newly revised theory, Einstein calculated that the bending of light by gravity would be twice as great, because of the effect produced by the curvature of spacetime. Therefore, the sun’s gravity would bend a beam by about 1.7 arc-seconds, he now predicted. It was a prediction that would have to wait for the next suitable eclipse, more than three years away, to be tested.
That very morning, November 18, Einstein received Hilbert’s new paper, the one that he had been invited to Göttingen to hear presented. Einstein was surprised, and somewhat dismayed, to see how similar it was to his own work. His response to Hilbert was terse, a bit cold, and clearly designed to assert the priority of his own work:
The system you furnish agrees—as far as I can see—exactly with what I found in the last few weeks and have presented to the Academy. The difficulty was not in finding generally covariant equations ...for this is easily achieved with Riemann’s tensor . . . Three years ago with my friend Grossmann I had already taken into consideration the only covariant equations, which have now been shown to be the correct ones. We had distanced ourselves from it, reluctantly, because it seemed to me that the physical discussion yielded an incongruity with Newton’s law. Today I am presenting to the Academy a paper in which I derive quantitatively out of general relativity, without any guiding hypothesis, the perihelion motion of Mercury. No gravitational theory has achieved this until now.80
Hilbert responded kindly and quite generously the following day, claiming no priority for himself. “Cordial congratulations on conquering perihelion motion,” he wrote. “If I could calculate as rapidly as you, in my equations the electron would have to capitulate and the hydrogen atom would have to produce its note of apology about why it does not radiate.”81
Yet the day after, on November 20, Hilbert sent in a paper to a Göttingen science journal proclaiming his own version of the equations for general relativity. The title he picked for his piece was not a modest one. “The Foundations of Physics,” he called it.
It is not clear how carefully Einstein read the paper that Hilbert sent him or what in it, if anything, affected his thinking as he busily prepared his climactic fourth lecture at the Prussian Academy. Whatever the case, the calculations he had done the week earlier, on Mercury and on light deflection, helped him realize that he could avoid the constraints and coordinate conditions he had been imposing on his gravitational field equations. And thus he produced in time for his final lecture—“The Field Equations of Gravitation,” on November 25, 1915—a set of covariant equations that capped his general theory of relativity.
The result was not nearly as vivid to the layman as, say, E=mc2. Yet using the condensed notations of tensors, in which sprawling complexities can be compressed into little subscripts, the crux of the final Einstein field equations is compact enough to be emblazoned, as it indeed often has been, on T-shirts designed for proud physics students. In one of its many variations,82 it can be written as:
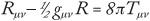
The left side of the equation starts with the term Rmn, which is the Ricci tensor he had embraced earlier. The term gmn is the all-important metric tensor, and the term R is the trace of the Ricci tensor called the Ricci scalar. Together, this left side of the equation—which is now known as the Einstein tensor and can be written simply as Gmn—compresses together all of the information about how the geometry of spacetime is warped and curved by objects.
The right side describes the movement of matter in the gravitational field. The interplay between the two sides shows how objects curve spacetime and how, in turn, this curvature affects the motion of objects. As the physicist John Wheeler has put it, “Matter tells space-time how to curve, and curved space tells matter how to move.”83
Thus is staged a cosmic tango, as captured by another physicist, Brian Greene:
Space and time become players in the evolving cosmos. They come alive. Matter here causes space to warp there, which causes matter over here to move, which causes space way over there to warp even more, and so on. General relativity provides the choreography for an entwined cosmic dance of space, time, matter, and energy.84
At last Einstein had equations that were truly covariant and thus a theory that incorporated, at least to his satisfaction, all forms of motion, whether it be inertial, accelerated, rotational, or arbitrary. As he proclaimed in the formal presentation of his theory that he published the following March in the Annalen der Physik, “The general laws of nature are to be expressed by equations that hold true for all systems of coordinates, that is they are covariant with respect to any substitutions whatever.”85
Einstein was thrilled by his success, but at the same time he was worried that Hilbert, who had presented his own version five days earlier in Göttingen, would be accorded some of the credit for the theory. “Only one colleague has really understood it,” he wrote to his friend Heinrich Zangger, “and he is seeking to nostrify it (Abraham’s expression) in a clever way.” The expression “to nostrify” (nostrifizieren), which had been used by the Göttingen-trained mathematical physicist Max Abraham, referred to the practice of nostrification by which German universities converted degrees granted by other universities into degrees of their own. “In my personal experience I have hardly come to know the wretchedness of mankind better.” In a letter to Besso a few days later, he added, “My colleagues are acting hideously in this affair. You will have a good laugh when I tell you about it.”86
So who actually deserves the primary credit for the final mathematical equations? The Einstein-Hilbert priority issue has generated a small but intense historical debate, some of which seems at times to be driven by passions that go beyond mere scientific curiosity. Hilbert presented a version of his equations in his talk on November 16 and a paper that he dated November 20, before Einstein presented his final equations on November 25. However, a team of Einstein scholars in 1997 found a set of proof pages of Hilbert’s article, on which Hilbert had made revisions that he then sent back to the publisher on December 16. In the original version, Hilbert’s equations differed in a small but important way from Einstein’s final version of the November 25 lecture. They were not actually generally covariant, and he did not include a step that involved contracting the Ricci tensor and putting the resulting trace term, the Ricci scalar, into the equation. Einstein did this in his November 25 lecture. Apparently, Hilbert made a correction in the revised version of his article to match Einstein’s version. His revisions, quite generously, also added the phrase “first introduced by Einstein” when he referred to the gravitational potentials.
Hilbert’s advocates (and Einstein’s detractors) respond with a variety of arguments, including that the page proofs are missing one part and that the trace term at issue was either unnecessary or obvious.
It is fair to say that both men—to some extent independently but each also with knowledge of what the other was doing—derived by November 1915 mathematical equations that gave formal expression to the general theory. Judging from Hilbert’s revisions to his own page proofs, Einstein seems to have published the final version of these equations first. And in the end, even Hilbert gave Einstein credit and priority.
Either way, it was, without question, Einstein’s theory that was being formalized by these equations, one that he had explained to Hilbert during their time together in Göttingen that summer. Even the physicist Kip Thorne, one of those who give Hilbert credit for producing the correct field equations, nonetheless says that Einstein deserves credit for the theory underlying the equations. “Hilbert carried out the last few mathematical steps to its discovery independently and almost simultaneously with Einstein, but Einstein was responsible for essentially everything that preceded these steps,” Thorne notes. “Without Einstein, the general relativistic laws of gravity might not have been discovered until several decades later.”87
Hilbert, graciously, felt the same way. As he stated clearly in the final published version of his paper, “The differential equations of gravitation that result are, as it seems to me, in agreement with the magnificent theory of general relativity established by Einstein.” Henceforth he would always acknowledge (thus undermining those who would use him to diminish Einstein) that Einstein was the sole author of the theory of relativity.88 “Every boy in the streets of Göttingen understands more about four-dimensional geometry than Einstein,” he reportedly said. “Yet, in spite of that, Einstein did the work and not the mathematicians.”89
Indeed, Einstein and Hilbert were soon friendly again. Hilbert wrote in December, just weeks after their dash for the field equations was finished, to say that with his support Einstein had been elected to the Göttingen Academy. After expressing his thanks, Einstein added, “I feel compelled to say something else to you.” He explained:
There has been a certain ill-feeling between us, the cause of which I do not want to analyze. I have struggled against the feeling of bitterness attached to it, with complete success. I think of you again with unmixed geniality and ask you to try to do the same with me. It is a shame when two real fellows who have extricated themselves somewhat from this shabby world do not afford each other mutual pleasure.90
They resumed their regular correspondence, shared ideas, and plotted to get a job for the astronomer Freundlich. By February Einstein was even visiting Göttingen again and staying at Hilbert’s home.
Einstein’s pride of authorship was understandable. As soon as he got printed copies of his four lectures, he mailed them out to friends. “Be sure you take a good look at them,” he told one. “They are the most valuable discovery of my life.” To another he noted, “The theory is of incomparable beauty.”91
Einstein, at age 36, had produced one of history’s most imaginative and dramatic revisions of our concepts about the universe. The general theory of relativity was not merely the interpretation of some experimental data or the discovery of a more accurate set of laws. It was a whole new way of regarding reality.
Newton had bequeathed to Einstein a universe in which time had an absolute existence that tick-tocked along independent of objects and observers, and in which space likewise had an absolute existence. Gravity was thought to be a force that masses exerted on one another rather mysteriously across empty space. Within this framework, objects obeyed mechanical laws that had proved remarkably accurate—almost perfect—in explaining everything from the orbits of the planets, to the diffusion of gases, to the jiggling of molecules, to the propagation of sound (though not light) waves.
With his special theory of relativity, Einstein had shown that space and time did not have independent existences, but instead formed a fabric of spacetime. Now, with his general version of the theory, this fabric of spacetime became not merely a container for objects and events. Instead, it had its own dynamics that were determined by, and in turn helped to determine, the motion of objects within it—just as the fabric of a trampoline will curve and ripple as a bowling ball and some billiard balls roll across it, and in turn the dynamic curving and rippling of the trampoline fabric will determine the path of the rolling balls and cause the billiard balls to move toward the bowling ball.
The curving and rippling fabric of spacetime explained gravity, its equivalence to acceleration, and, Einstein asserted, the general relativity of all forms of motion.92 In the opinion of Paul Dirac, the Nobel laureate pioneer of quantum mechanics, it was “probably the greatest scientific discovery ever made.” Another of the great giants of twentieth-century physics, Max Born, called it “the greatest feat of human thinking about nature, the most amazing combination of philosophical penetration, physical intuition and mathematical skill.”93
The entire process had exhausted Einstein but left him elated. His marriage had collapsed and war was ravaging Europe, but Einstein was as happy as he would ever be. “My boldest dreams have now come true,” he exulted to Besso. “General covariance. Mercury’s perihelion motion wonderfully precise.” He signed himself “contented but kaput.”94