谈到最X的数学公式(X处一般可以随意填),人们一般都会谈到欧拉关于复数指数的一个恒等式:
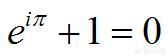
因为这个公式联系了世界上五个最重要的数字:表示什么都没有的0,表示一个的1,圆周率的π,自然对数的底e和虚数单位i,这个公式如此的简洁,但是在数学中又如此的重要,凡是学习了欧拉公式的人无不惊叹于欧拉深邃的思想。
为了了解它,首先我们要从“数系”的拓展开始。
自然数
在人们的生产和生活过程中,逐渐对数字产生了需求。人们为了给牛羊等牲畜计数,产生了自然数的概念。自然数就是全体正整数,也就是一个集合{1,2,3,4…} (有些教材把0也归类为自然数)。
自然数集合对加法是封闭的。所谓封闭,就是说如果A和B都是自然数,那么A+B也是自然数。例如2+3=5,4+6=10。 但是,自然数对减法不是封闭的,也就是说,如果A和B都是自然数,A-B不一定是自然数。例如3-2=1还是自然数,但是5-8=-3就不是自然数了。
整数
也许曾经有一段时间,人们认为5-8是没有意义的。就好像“我一共有5只羊,但是却要杀8只羊招待客人,还剩下几只羊?”这种问题根本不会发生。
但实际上,只要我们去别人家借三只羊就可以满足要求,此时我们拥有的羊就变成了负债3只。也就是-3的含义。所以,人们又发明了0 和负整数。正整数,零和负整数合成了整数集合{……-4,-3,-2,-1,0,1,2,3,4……}
整数对加减法都是封闭的,对乘法也是封闭的,但是对除法就不封闭了。也就是说,如果A和B都是整数,A÷B就不一定是整数。例如4÷2=2是整数,但是3÷2=1.5就不是整数。
有理数
为了解决除法封闭性的问题,人们发明了分数。在4000年前,古埃及人和古希腊人就在使用分数了。公元前5世纪,古希腊数学家毕达哥拉斯将整数和分数合在一起,提出了有理数的概念。
所谓有理数,就是可以写成两个整数的比的数。写作集合就是
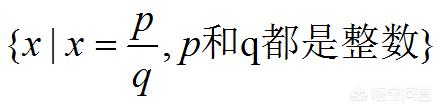
这样一来,有理数的加、减、乘、除(分母不能为零)就都封闭了。
毕达哥拉斯等人沉醉于自己的成就,他们认为所有的数字都是有理数。但是很快,学派内部的学者希帕索斯就发现了问题:如果一个直角三角形的两个直角边都是1,那么斜边无法用两个整数的比来表示。并由此引发了第一次数学危机。
这个问题在于,有理数对于开方运算是不封闭的,例如:√4=2是有理数,但是√2就不是有理数。
实数
人们经过长期的研究,终于发现不仅有可以表示成两个整数的比的有理数,还有不能表示成整数比的无限不循环小数:无理数。人们把有理数和无理数合在一起,称为实数。实数与数轴上的点一一对应。
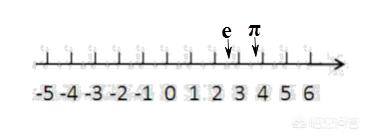
在数轴上,我们不仅能找到整数1、2、3…,还能找到分数2/3,也能找到e、π、√2等无理数。
但是,数系并没有到此结束。因为人们发现√-1还是无法在实数范围内找到答案。也许有人会说:这个数本身就不存在啊!任何一个数的平方都一定是非负的,所以怎么会有一个数字的平方等于-1呢?
复数
数学家们并不这样认为。他们觉得这个数字就好像5-8一样,在某个时刻就会找到它的用处。的确,现在的物理学和数学中,这个数字的作用非常大。这就是虚数。
人们定义虚数单位i的含义是i=√-1,也就是说:
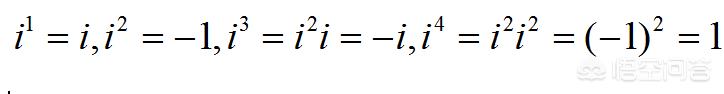
i每4次幂循环一次。我们按照这个规律可以计算出i的2018次幂等于-1。
实数和虚数可以合在一起,就构成了复数:形如a+bi的数字,其中a和b都是实数,而i是虚数单位。
复数可以用复平面上的一个点(或者一个有向线段)表示。
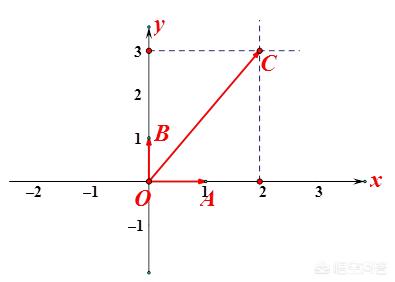
复平面是由实轴(OX轴)和虚轴(OY轴)构成的平面。实轴就是实数轴,上面的每一个点表示一个实数,例如A点就表示1。虚轴是一个少了原点的数轴,每一个点表示一个虚数,例如B点就表示i。那么平面上的C点在实轴上投影为2,在虚轴上投影为3,所以C点表示的复数就是2+3i.
复数的加减乘除规则与实数非常类似。例如:
A=1+i, B=2+3i, 则
A+B=3+4i; A-B=-1-2i,A×B=(2-3)+(2+3)i=-1+5i等。
显然,复数内的加减乘除(分母不为零)都是封闭的,而且复数的实数次幂也是复数。
不过,问题也接踵而至:一个数的复数次幂是什么?
欧拉公式
一个整数的有理数幂很简单
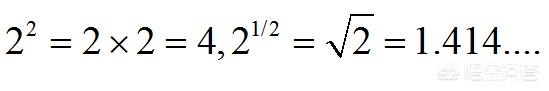
对于无理数幂,例如2的π次幂,我们总可以用两个有理数去逼近,也就是说我们知道
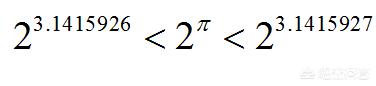
只要我们愿意,总可以把精度无限提高,这样无理数幂次的含义也被我们弄清楚了。
可是,2的i次幂到底是什么?人们仿佛毫无头绪。直到欧拉出现了。欧拉提出了著名的欧拉公式:
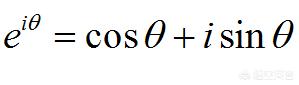
其中θ是一个实数,e是自然对数的底2.71828…
利用这个公式,我们就可以计算一个数的复数次幂了。例如:
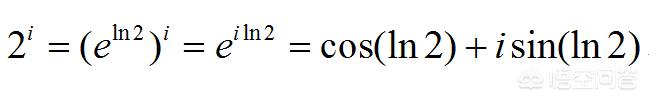
其中ln2表示以e为底2的对数,它是一个实数。
有了这个公式,复数在乘方上也封闭起来了。而且,如果我们令θ=π代入公式,就会得到
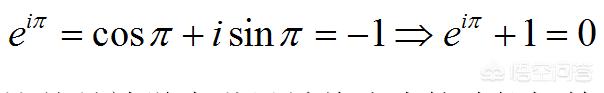
这就是被誉为世界最美公式的欧拉恒等式。
欧拉公式的证明和应用
欧拉公式有许多证明方法,比如可以使用泰勒展开。
泰勒展开公式是说:一个光滑的函数可以展开成一系列函数的形式。例如e^x、cosx和sinx可以分别展开成下列形式:
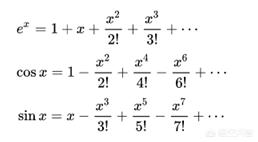
我们把x=iθ代入上述公式,就可以发现欧拉公式的左右两边相等。此外还有求导、积分等方法。
使用欧拉公式可以解决非常多的问题,尤其在实变函数和物理中电学问题里,经常会把一个三角函数写作复数形式进行求解。没有欧拉,我们很难解决交流电中的许多计算,也难以实现大规模的电气化。
顺便一说,1783年,76岁的欧拉在一起和家人聚餐,在陪孙子玩的时候他突然停下,对大家说:我死了。然后就与世长辞了。欧拉用自己的生命证明了:一个真正的数学家是没有什么不能预测的。
1、雅各布线:纵使改变,依然故我
![]()

关于雅各布线,最为人们津津乐道的轶事之一,是雅各布醉心于研究对数螺线,这项研究从1691年就开始了。他发现,对数螺线经过各种变换后仍然是对数螺线,如它的渐屈线和渐伸线是对数螺线,自极点至切线的垂足的轨迹,以极点为发光点经对数螺线反射后得到的反射线,以及与所有这些反射线相切的曲线(回光线)都是对数螺线。他惊叹这种曲线的神奇,竟在遗嘱里要求后人将对数螺线刻在自己的墓碑上,并附以颂词“纵然变化,依然故我”,用以象征死后永生不朽。
2、阿基米德线
![]()
据说,阿基米德螺线最初是由阿基米德的老师柯农(欧几里德的弟子)发现的。柯农死后,阿基米德继续研究,又发现许多重要性质,因而这种螺线就以阿基米德的名字命名了。
3、圆线
![]()

关于圆线的公式,这里就不说了。
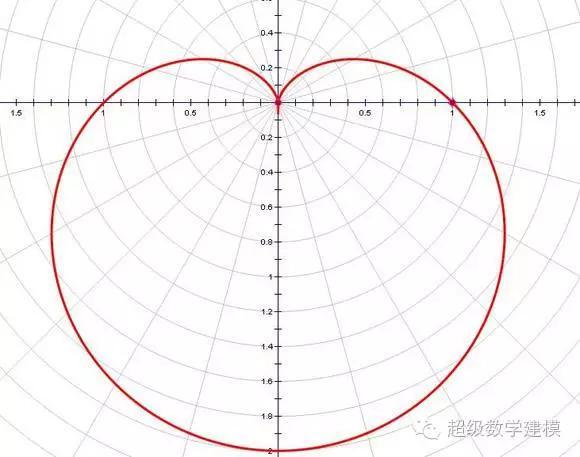
4、心形线
![]()
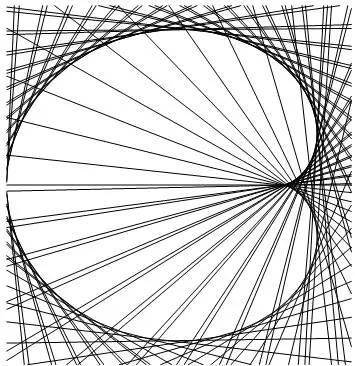
法国数学家笛卡尔在1649年欧洲大陆爆发黑死病时流浪到瑞典,在斯德哥尔摩的街头,52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。几天后,他意外的接到通知,国王聘请他做小公主的数学老师。跟随前来通知的侍卫一起来到皇宫,他见到了在街头偶遇的女孩子。从此,他当上了小公主的数学老师。
小公主的数学在笛卡尔的悉心指导下突飞猛进,笛卡尔向她介绍了自己研究的新领域——直角坐标系。每天形影不离的相处使他们彼此产生爱慕之心,公主的父亲国王知道了后勃然大怒,下令将笛卡尔处死,小公主克里斯汀苦苦哀求后,国王将其流放回法国,克里斯汀公主也被父亲软禁起来。
笛卡尔回法国后不久便染上重病,他日日给公主写信,因被国王拦截,克里斯汀一直没收到笛卡尔的信。笛卡尔在给克里斯汀寄出第十三封信后就气绝身亡了,这第十三封信内容只有短短的一个公式:r=a(1-sinθ)。
国王看不懂,觉得他们俩之间并不是总是说情话的,将全城的数学家召集到皇宫,但没有一个人能解开,他不忍心看着心爱的女儿整日闷闷不乐,就把这封信交给一直闷闷不乐的克里斯汀。
公主看到后,立即明了恋人的意图,她马上着手把方程的图形画出来,一颗心形图案出现在眼前,克里斯汀不禁流下感动的泪水,这条曲线就是著名的“心形线”。
国王死后,克里斯汀登基,立即派人在欧洲四处寻找心上人,无奈斯人已故,先她一步走了,徒留她孤零零在人间......据说这封享誉世界的另类情书还保存在欧洲笛卡尔的纪念馆里。
虽然这个故事是假的。。。
5、玫瑰线
![]()
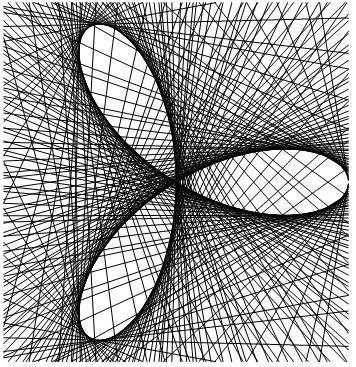
玫瑰线的说法源于欧洲海图。在中世纪的 航海地图上,并没有 经纬线,有的只是一些从中心有序地向外辐射的互相交叉的直线方向线。此线也称罗盘线, 希腊神话里的各路风神被精心描绘在这些线上,作为方向的记号。所以,哥伦布探险队中的西班牙水手想到方向的时候,并不是罗盘方位上的多少度,而是风(losvientos)。而葡萄牙水手则称他们的罗盘盘面为风的玫瑰(rosedosventor)。水手们根据太阳的位置估计风向,再与“ 风玫瑰”对比找出航向。玫瑰线,即指引方向的线。
6、线性方程
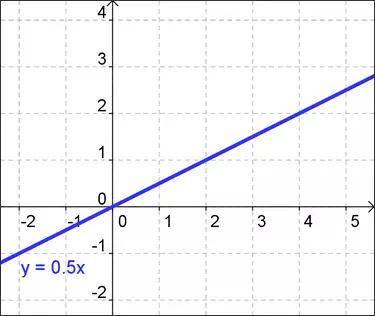
大道至简,化繁为简!![]() 线性方程事实上是人类最喜欢的含未知数的公式,因为其中之包含乘法与加法,简单地不可挑剔。
线性方程事实上是人类最喜欢的含未知数的公式,因为其中之包含乘法与加法,简单地不可挑剔。