什么是内存
内存(Memory)是计算机中最重要的部件之一,它是程序与CPU进行沟通的桥梁。计算机中所有程序的运行都是在内存中进行的,因此内存对计算机的影响非常大,内存又被称为主存,其作用是存放 CPU 中的运算数据,以及与硬盘等外部存储设备交换的数据。只要计算机在运行中,CPU 就会把需要运算的数据调到主存中进行运算,当运算完成后CPU再将结果传送出来,主存的运行也决定了计算机的稳定运行。
内存的物理结构
在了解一个事物之前,你首先得先需要见过它,你才会有印象,才会有想要了解的兴趣,所以我们首先需要先看一下什么是内存以及它的物理结构是怎样的。

内存的内部是由各种IC电路组成的,它的种类很庞大,但是其主要分为三种存储器
- 随机存储器(RAM): 内存中最重要的一种,表示既可以从中读取数据,也可以写入数据。当机器关闭时,内存中的信息会丢失。
- 只读存储器(ROM):ROM 一般只能用于数据的读取,不能写入数据,但是当机器停电时,这些数据不会丢失。
- 高速缓存(Cache):Cache 也是我们经常见到的,它分为一级缓存(L1 Cache)、二级缓存(L2 Cache)、三级缓存(L3 Cache)这些数据,它位于内存和 CPU 之间,是一个读写速度比内存更快的存储器。当 CPU 向内存写入数据时,这些数据也会被写入高速缓存中。当 CPU 需要读取数据时,会直接从高速缓存中直接读取,当然,如需要的数据在Cache中没有,CPU会再去读取内存中的数据。

图中 VCC 和 GND 表示电源,A0 - A9 是地址信号的引脚,D0 - D7 表示的是数据信号、RD 和 WR 都是控制信号,我用不同的颜色进行了区分,将电源连接到 VCC 和 GND 后,就可以对其他引脚传递 0 和 1 的信号,大多数情况下,+5V 表示1,0V 表示 0。
我们都知道内存是用来存储数据,那么这个内存 IC 中能存储多少数据呢?D0 - D7 表示的是数据信号,也就是说,一次可以输入输出 8 bit = 1 byte 的数据。A0 - A9 是地址信号共十个,表示可以指定 00000 00000 - 11111 11111 共 2 的 10次方 = 1024个地址。每个地址都会存放 1 byte 的数据,因此我们可以得出内存 IC 的容量就是 1 KB。
如果我们使用的是 512 MB 的内存,这就相当于是 512000(512 * 1000) 个内存 IC。当然,一台计算机不太可能有这么多个内存 IC ,然而,通常情况下,一个内存 IC 会有更多的引脚,也就能存储更多数据。
内存的读写过程
让我们把关注点放在内存 IC 对数据的读写过程上来吧!我们来看一个对内存IC 进行数据写入和读取的模型
来详细描述一下这个过程,假设我们要向内存 IC 中写入 1byte 的数据的话,它的过程是这样的:
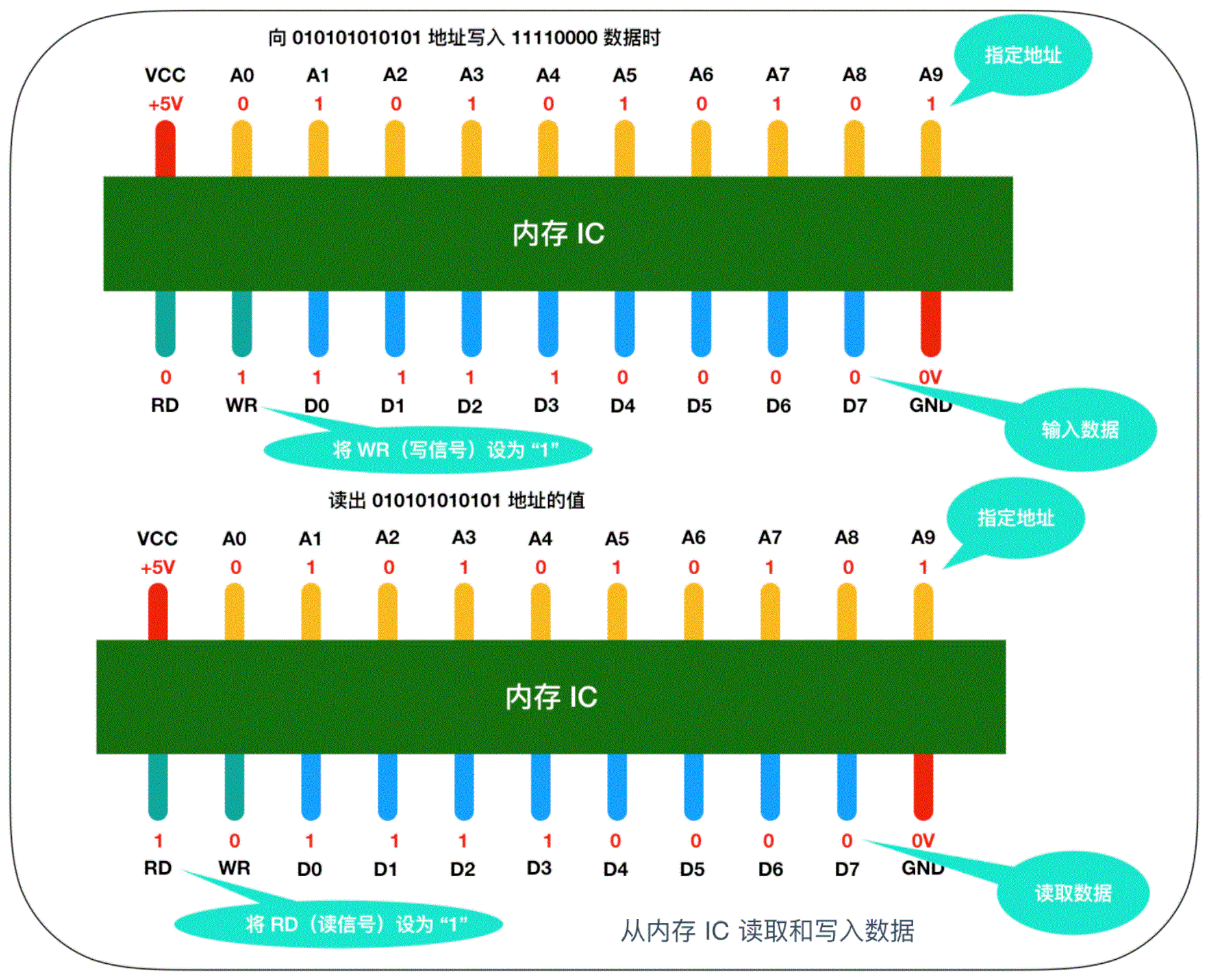
- 首先给 VCC 接通 +5V 的电源,给 GND 接通 0V 的电源,使用 A0 - A9 来指定数据的存储场所,然后再把数据的值输入给 D0 - D7 的数据信号,并把 WR(write)的值置为 1,执行完这些操作后,即可以向内存 IC 写入数据
- 读出数据时,只需要通过 A0 - A9 的地址信号指定数据的存储场所,然后再将 RD 的值置为 1 即可。
- 图中的 RD 和 WR 又被称为控制信号。其中当WR 和 RD 都为 0 时,无法进行写入和读取操作。
为了便于记忆,我们把内存模型映射成为我们现实世界的模型,在现实世界中,内存的模型很想我们生活的楼房。在这个楼房中,1层可以存储一个字节的数据,楼层号就是地址,下面是内存和楼层整合的模型图
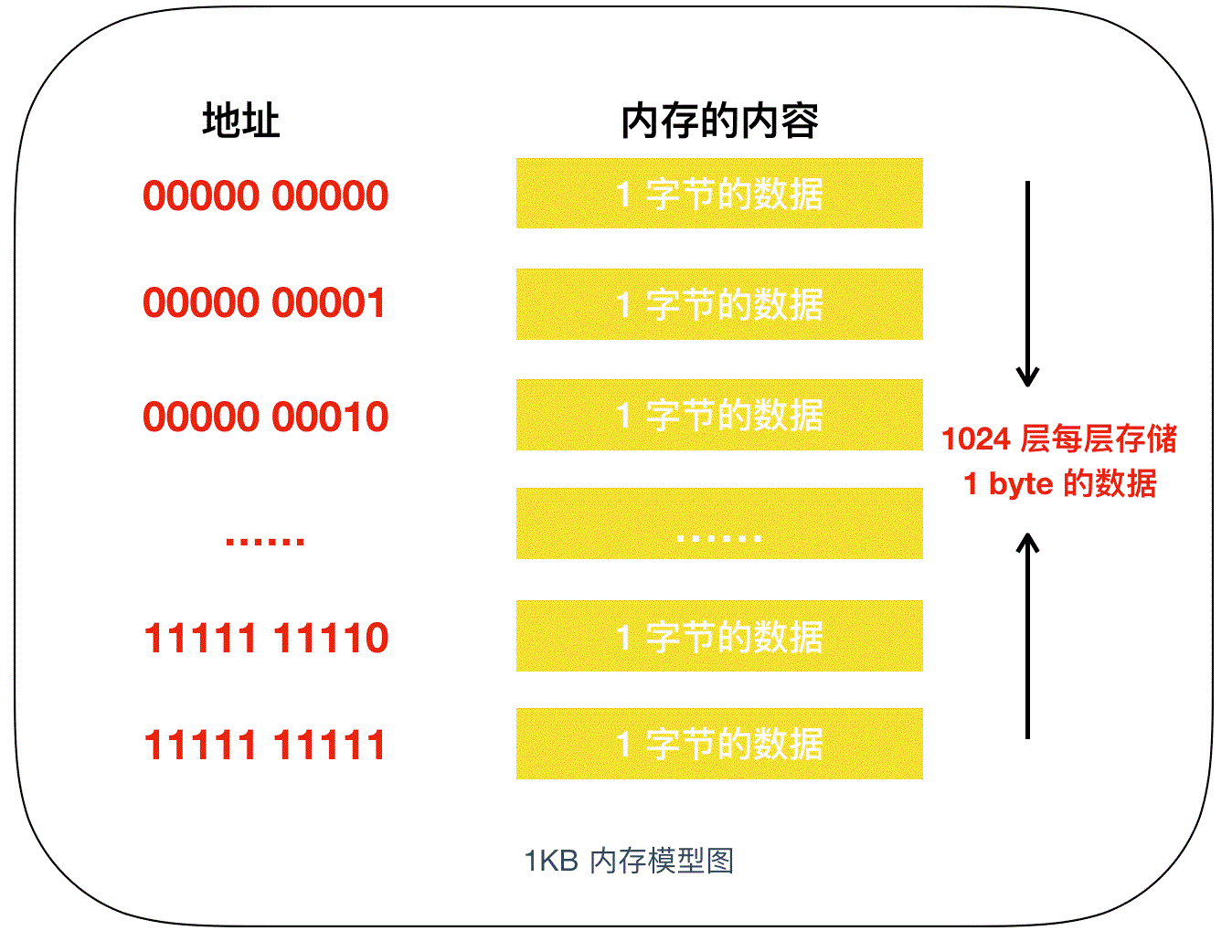
我们知道,程序中的数据不仅只有数值,还有数据类型的概念,从内存上来看,就是占用内存大小(占用楼层数)的意思。即使物理上强制以 1 个字节为单位来逐一读写数据的内存,在程序中,通过指定其数据类型,也能实现以特定字节数为单位来进行读写。
下面是一个以特定字节数为例来读写指令字节的程序的示例
// 定义变量 char a; short b; long c; // 变量赋值 a = 123; b = 123; c = 123;
我们分别声明了三个变量 a,b,c ,并给每个变量赋上了相同的 123,这三个变量表示内存的特定区域。通过变量,即使不指定物理地址,也可以直接完成读写操作,操作系统会自动为变量分配内存地址。
这三个变量分别表示 1 个字节长度的 char,2 个字节长度的 short,表示4 个字节的 long。因此,虽然数据都表示的是 123,但是其存储时所占的内存大小是不一样的。如下所示

这里的 123 都没有超过每个类型的最大长度,所以 short 和 long 类型为所占用的其他内存空间分配的数值是0,这里我们采用的是低字节序列的方式存储。
低字节序列:将数据低位存储在内存低位地址。
高字节序列:将数据的高位存储在内存地位的方式称为高字节序列。
内存的使用
指针
指针是 C 语言非常重要的特征,指针也是一种变量,只不过它所表示的不是数据的值,而是内存的地址。通过使用指针,可以对任意内存地址的数据进行读写。
在了解指针读写的过程前,我们先需要了解如何定义一个指针,和普通的变量不同,在定义指针时,我们通常会在变量名前加一个 * 号。例如我们可以用指针定义如下的变量
char *d; // char类型的指针 d 定义 short *e; // short类型的指针 e 定义 long *f; // long类型的指针 f 定义
我们以32位计算机为例,32位计算机的内存地址是 4 字节,在这种情况下,指针的长度也是 32 位。然而,变量 d e f 却代表了不同的字节长度,这是为什么呢?
实际上,这些数据表示的是从内存中一次读取的字节数,比如 d e f 的值都为 100,那么使用 char 类型时就能够从内存中读写 1 byte 的数据,使用 short 类型就能够从内存读写 2 字节的数据, 使用 long 就能够读写 4 字节的数据,下面是一个完整的类型字节表
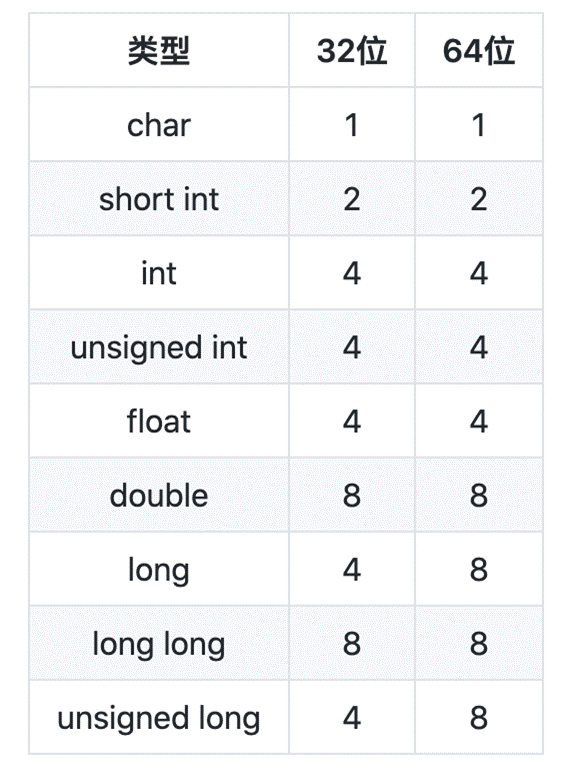
我们可以用图来描述一下这个读写过程
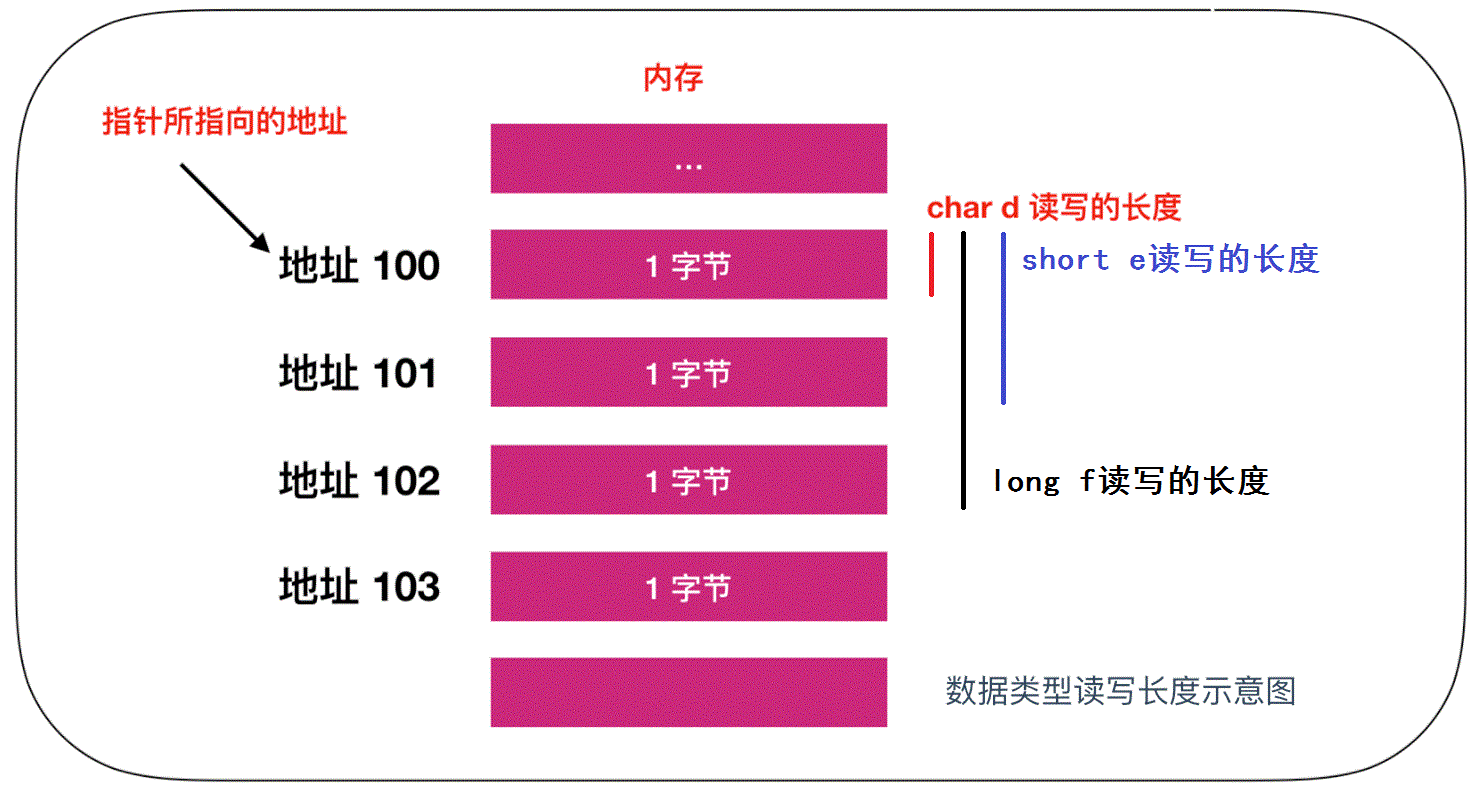
数组是内存的实现
数组是指多个相同的数据类型在内存中连续排列的一种形式。作为数组元素的各个数据会通过下标编号来区分,这个编号也叫做索引,如此一来,就可以对指定索引的元素进行读写操作。
首先先来认识一下数组,我们还是用 char、short、long 三种元素来定义数组,数组的元素用[value] 扩起来,里面的值代表的是数组的长度,就像下面的定义
char g[100]; short h[100]; long i[100];
数组定义的数据类型,也表示一次能够读写的内存大小,char 、short 、long 分别以 1 、2 、4 个字节为例进行内存的读写。
数组是内存的实现,数组和内存的物理结构完全一致,尤其是在读写1个字节的时候,当字节数超过 1 时,只能通过逐个字节来读取,下面是内存的读写过程

数组是我们学习的第一个数据结构,我们都知道数组的检索效率是比较快的,至于数组的检索效率为什么这么快并不是我们这篇文章讨论的重点。
栈和队列
我们上面提到数组是内存的一种实现,使用数组能够使编程更加高效,下面我们就来认识一下其他数据结构,通过这些数据结构也可以操作内存的读写。
栈
栈(stack)是一种很重要的数据结构,栈采用 LIFO(Last In First Out)即后入先出的方式对内存进行操作。它就像一个大的收纳箱,你可以往里面放相同类型的东西,比如书,最先放进收纳箱的书在最下面,最后放进收纳箱的书在最上面,如果你想拿书的话, 必须从最上面开始取,否则是无法取出最下面的书籍的。
栈的数据结构就是这样,你把书籍压入收纳箱的操作叫做压入(push),你把书籍从收纳箱取出的操作叫做弹出(pop),它的模型图大概是这样
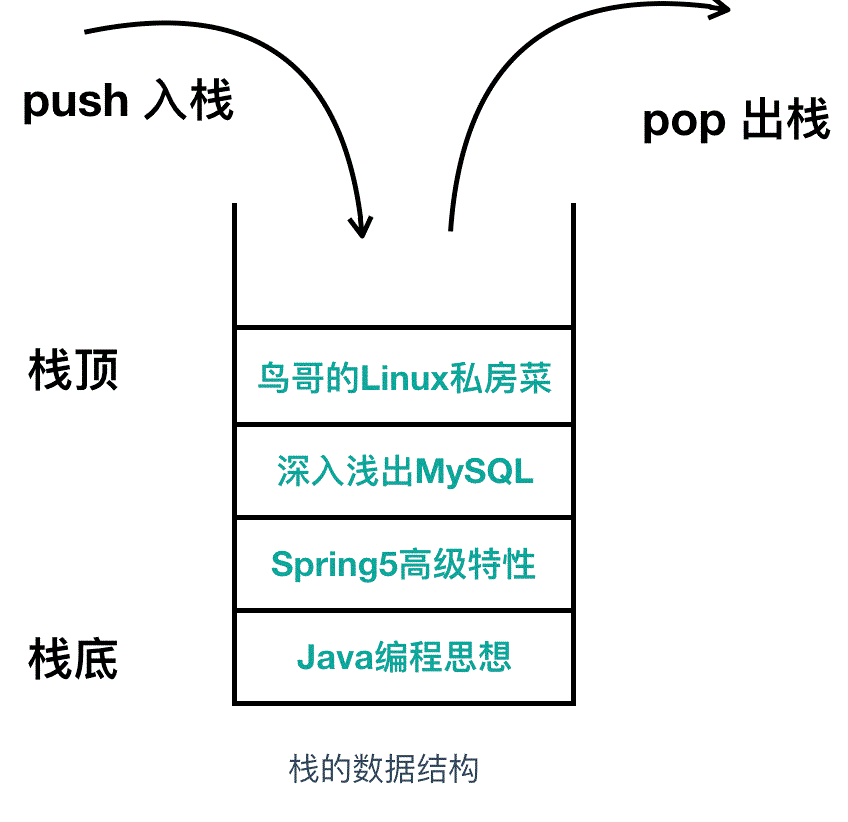
入栈相当于是增加操作,出栈相当于是删除操作,只不过叫法不一样。栈和内存不同,它不需要指定元素的地址。它的大概使用如下
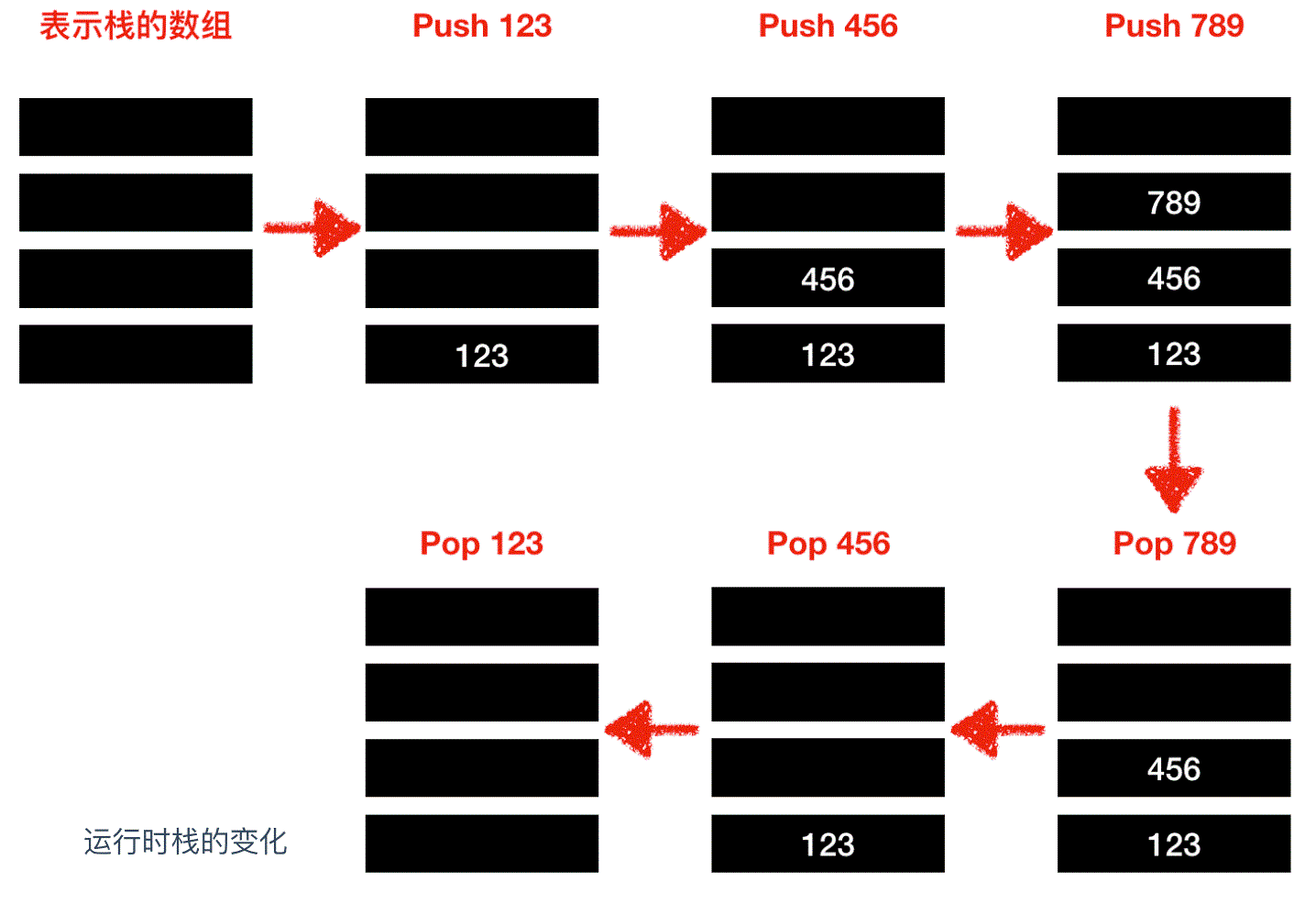
// 压入数据 Push(123); Push(456); Push(789); // 弹出数据 j = Pop(); k = Pop(); l = Pop();
在栈中,LIFO 方式表示栈的数组中所保存的最后面的数据(Last In)会被最先读取出来(First On)。
队列
队列和栈很相似但又不同,相同之处在于队列也不需要指定元素的地址,不同之处在于队列是一种 先入先出(First In First Out) 的数据结构。队列在我们生活中的使用很像是我们去景区排队买票一样,第一个排队的人最先买到票,以此类推,俗话说: 先到先得。它的使用如下
// 往队列中写入数据 EnQueue(123); EnQueue(456); EnQueue(789); // 从队列中读出数据 m = DeQueue(); n = DeQueue(); o = DeQueue();
向队列中写入数据称为 EnQueue()入列,从队列中读出数据称为DeQueue()。
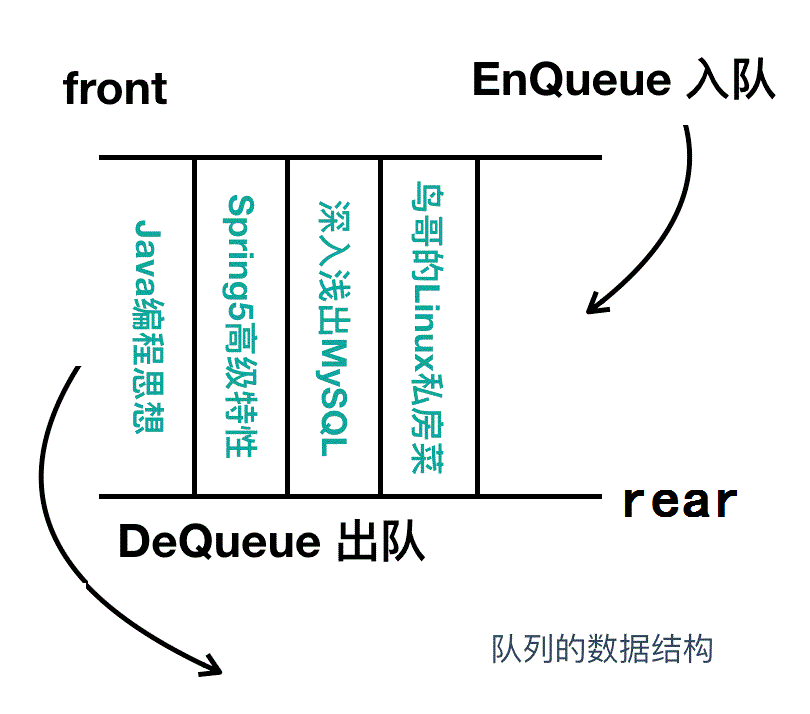
与栈相对,FIFO 的方式表示队列中最先所保存的数据会优先被读取出来。
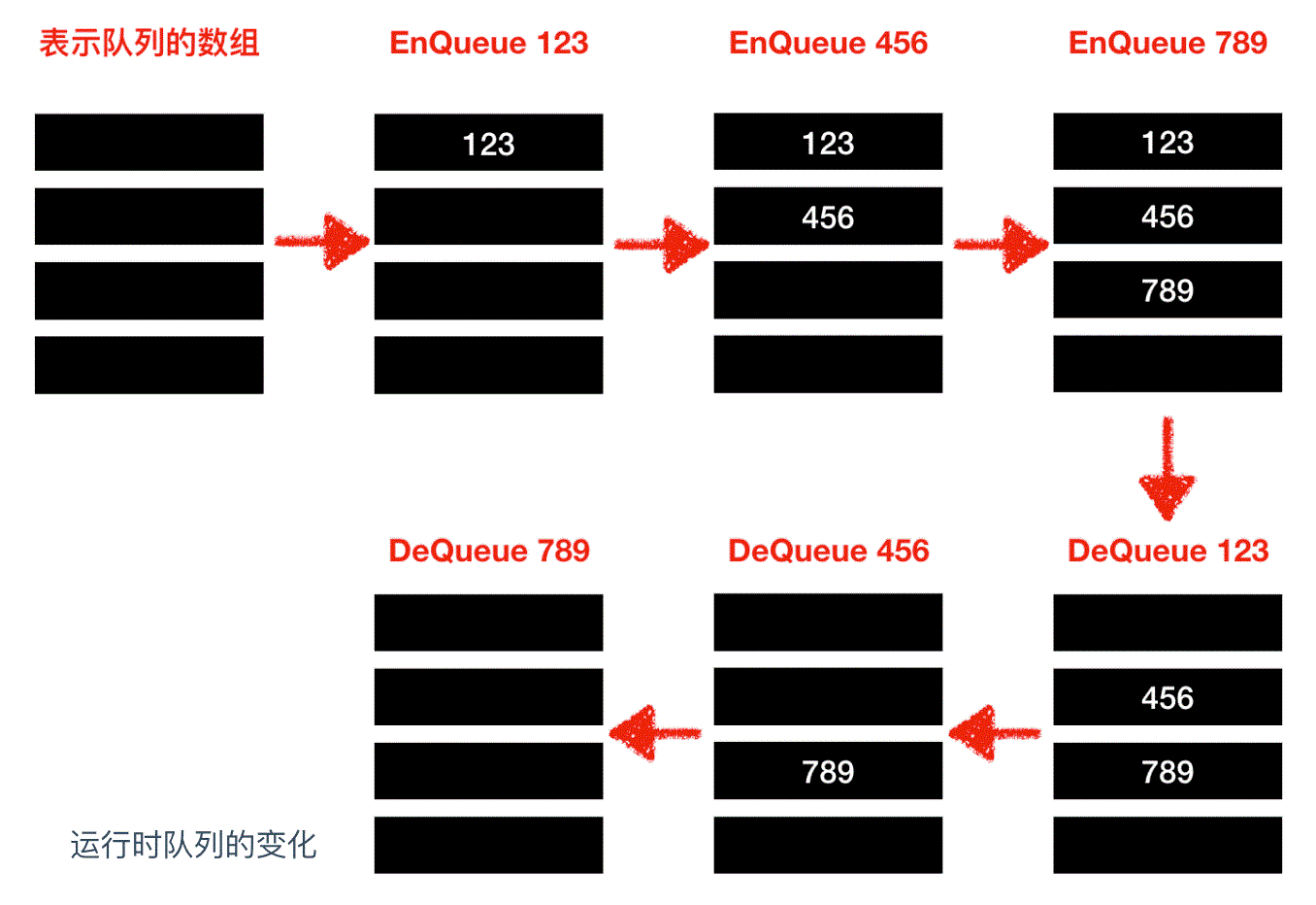
队列的实现一般有两种:顺序队列 和 循环队列,我们上面的事例使用的是顺序队列,那么下面我们看一下循环队列的实现方式
环形缓冲区
循环队列一般是以环状缓冲区(ring buffer)的方式实现的,它是一种用于表示一个固定尺寸、头尾相连的缓冲区的数据结构,适合缓存数据流。假如我们要用 6 个元素的数组来实现一个环形缓冲区,这时可以从起始位置开始有序的存储数据,然后再按照存储时的顺序把数据读出。在数组的末尾写入数据后,后一个数据就会从缓冲区的头开始写。这样,数组的末尾和开头就连接了起来。
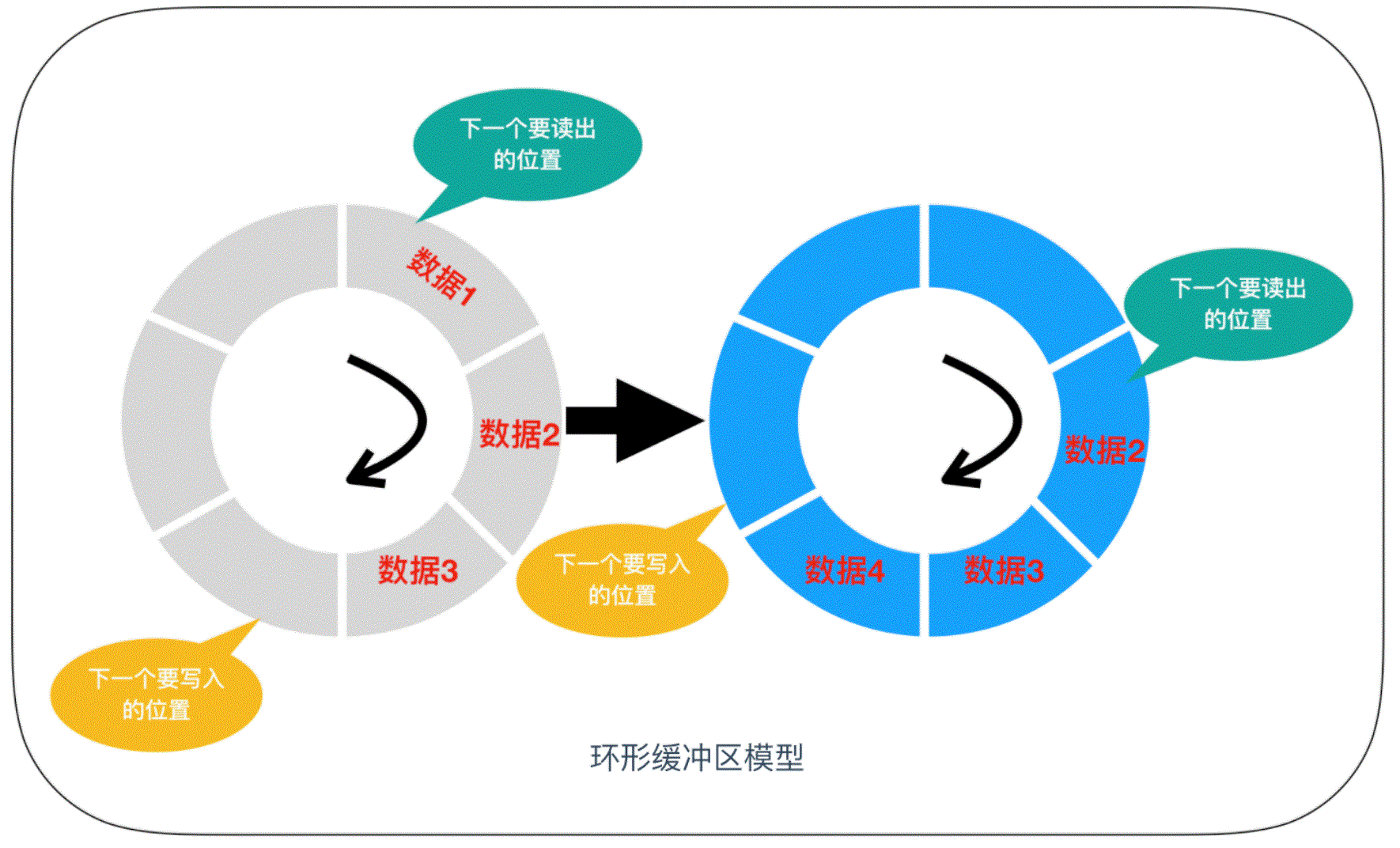
链表
下面我们来介绍一下链表和 二叉树,它们都是可以不用考虑索引的顺序就可以对元素进行读写的方式。通过使用链表,可以高效的对数据元素进行添加 和 删除操作。而通过使用二叉树,则可以更高效的对数据进行检索。
在实现数组的基础上,除了数据的值之外,通过为其附带上下一个元素的索引,即可实现链表。数据的值和下一个元素的地址(索引)就构成了一个链表元素,如下所示
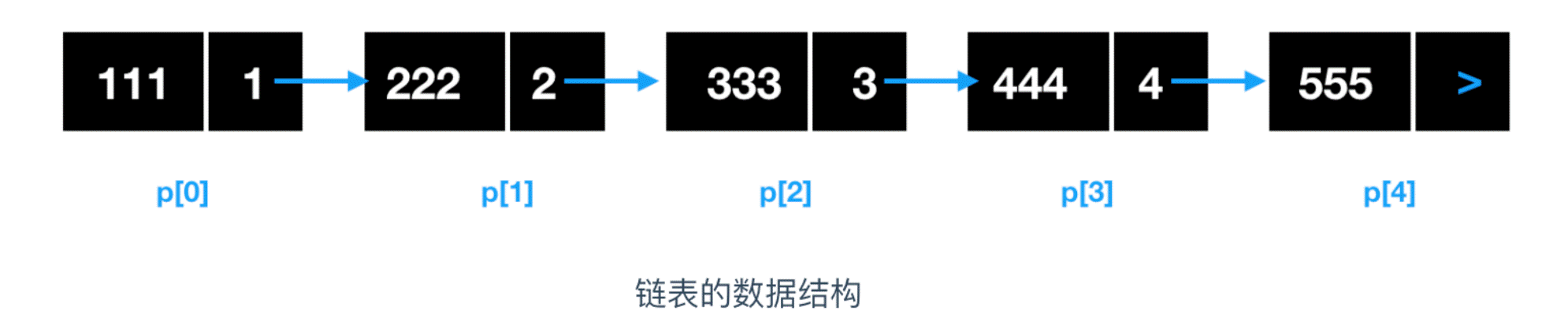
对链表的添加和删除都是非常高效的,我们来叙述一下这个添加和删除的过程,假如我们要删除地址为 p[2] 的元素,链表该如何变化呢?
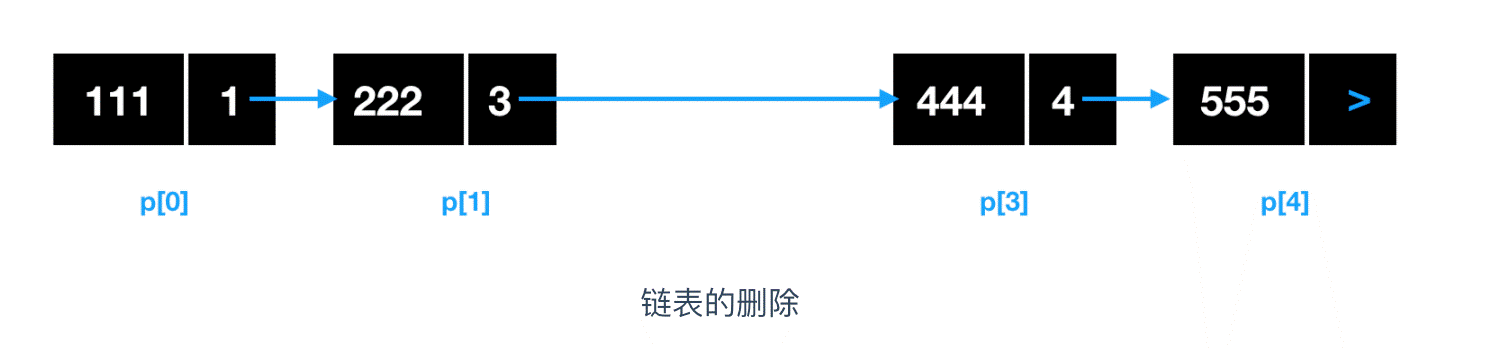
我们可以看到,删除地址为 p[2] 的元素后,直接将链表剔除,并把 p[2] 前一个位置的元素 p[1] 的指针域指向 p[2] 下一个链表元素的数据区即可。
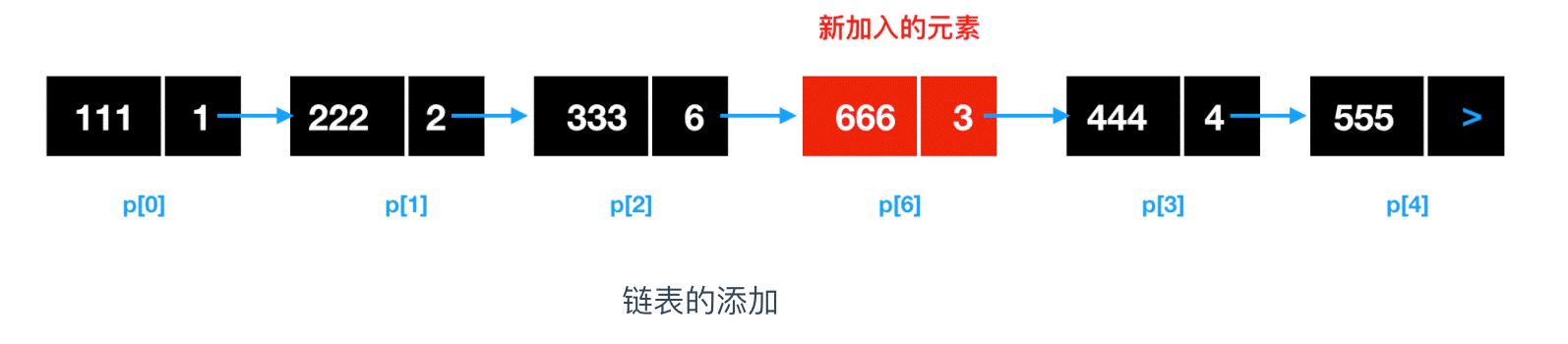
那么对于新添加进来的链表,需要确定插入位置,比如要在 p[2] 和 p[3] 之间插入地址为 p[6] 的元素,需要将 p[6] 的前一个位置 p[2] 的指针域改为 p[6] 的地址,然后将 p[6] 的指针域改为 p[3] 的地址即可。
链表的添加不涉及到数据的移动,所以链表的添加和删除很快,而数组的添加设计到数据的移动,所以比较慢,通常情况下,使用数组来检索数据,使用链表来进行添加和删除操作。
二叉树
二叉树也是一种检索效率非常高的数据结构,二叉树是指在链表的基础上往数组追加元素时,考虑到数组的大小关系,将其分成左右两个方向的表现形式。假如我们把 50 这个值保存到了数组中,那么,如果接下来要进行值写入的话,就需要和50比较,确定谁大谁小,比50数值大的放右边,小的放左边,下图是二叉树的比较示例
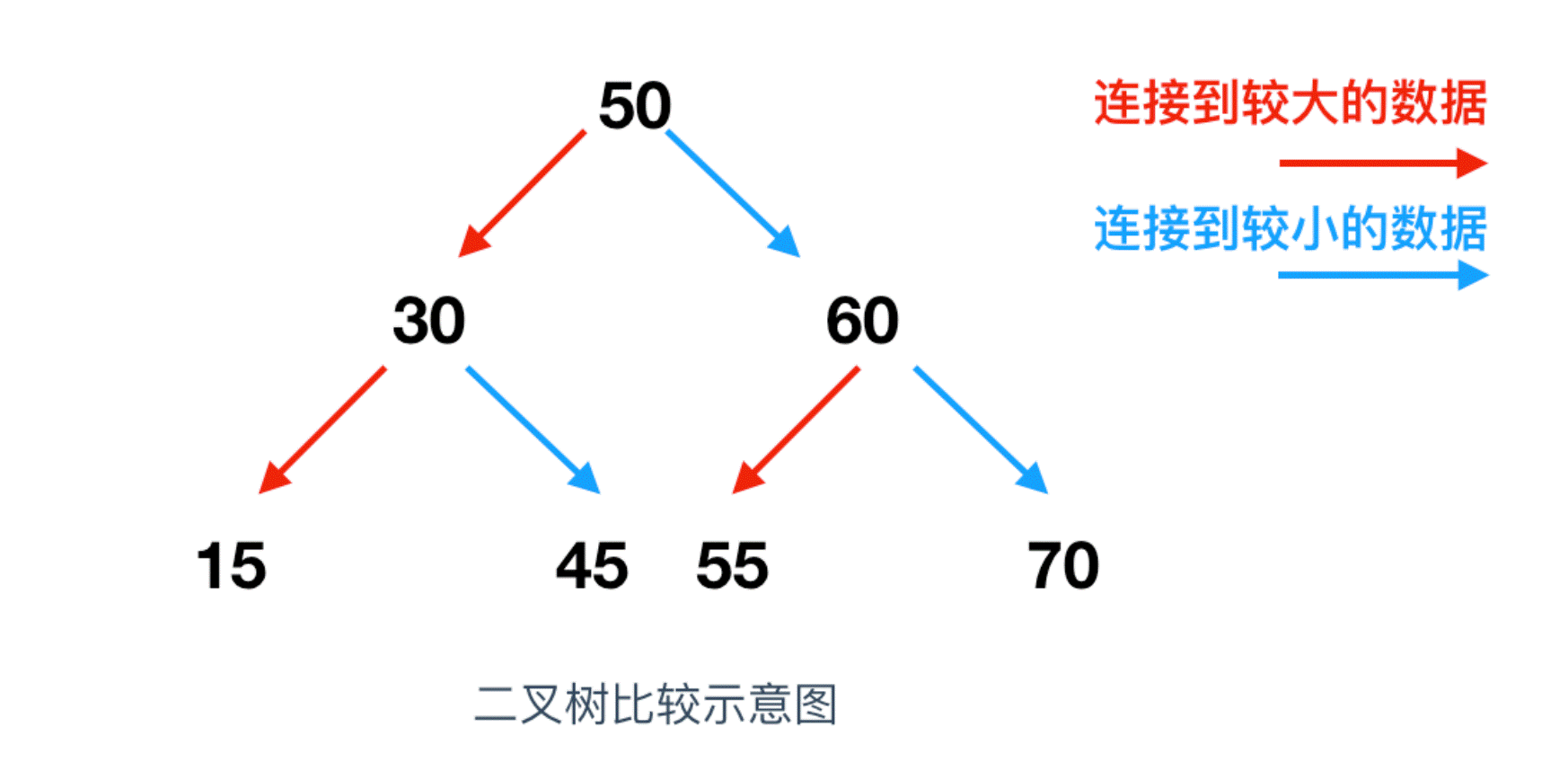
二叉树是由链表发展而来,因此二叉树在追加和删除元素方面也是同样有效的。
这一切的演变都是以内存为基础的。