12 位运算

大家知道，程序中的数据在内存中，都是以二进制的形式存在的。所以，内存中的数据一般都是0和1组成的序列。所谓位运算就是直接对整数在内存中补码的二进制位进行操作。直接对二进制位进行操作，使得位运算比普通的运算操作效率要高。

关于位运算的操作分为：与(and)，或(or)，取反(not)，异或(xor)，左移(shl)，右移(shr/sar)等几种运算，它们共同构成了C语言中的位运算操作。

12.1 二进制与位运算

程序中的数据在内存中，都是以二进制的形式存在的。所以，内存中的数据一般都是0和1组成的序列。所谓位运算就是直接对整数在内存中的二进制位进行操作。直接对二进制位进行操作，使得位运算比普通的运算操作效率要高。

如下图所示，数据是用字节表示的，1个字节占8位。位运算就是直接对字节中的位进行运算。关于位运算的操作分为：与(and)，或(or)，取反(not)，异或(xor)，左移(shl)，右移(shr/sar)等几种运算，它们共同构成了C语言中的位运算操作。

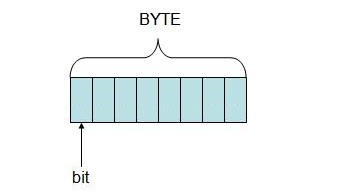
学习位运算的基础是掌握整数的补码存储与二进制表示方法，以及如何将一个十进制整数转化为二进制。详情请见第二章2.6/2.7节。

12.2 与（&）运算

与运算的操作符为&。2个数进行与运算时，就是将这2个数的二进制进行与操作，只有当2个数对应的位都为1，该位运算结果为1，否则运算结果为0。

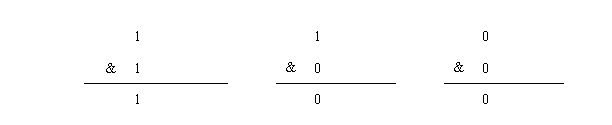
即1&1 = 1，1&0 = 0。那么如何计算两个整数的与运算呢？比如计算15&10，首先15的二进制为：1111，10的二进制为1010，所以15&10为：

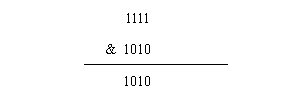
所以15&10=10。

int main(void)
{
    int a = 15;
    int b = 10;
    int c = 15&10;
    printf(“a&b=%d\n”, c);
    return 0;
}

12.3 与（&）运算的应用

与运算的性质：任何数&1都是它本身，&0是0。因此我们可以通过与运算来获取一个整数的某个部份的值，比如：

获取一个整数的后3位：

int x=100;

x&7即为x的后三位。因为7的二进制码为0111。所以，任何一个数与7进行与运算，那么其它位都会被置零。只有后三位得到保留。

我们也可以使用与运算与取反和移位运算相结合，将整数的某位置零。比如：

x&(~(1<<n))即可将x第n位置为零。

#define CLEARFLAG(a,n) ((a) &= ~(1<<(n)))//把整数a中第n位置为0

此外，我们还可以用来判断一个整数中某位是否为1（通常是某个标志信息），比如：

x&(1<<n);

上面的语句可以用来判断x中第n位是否为1。有时候一个整数通常用某1位或几位置1来表示一个信息，另几位表示另外的信息，这个时候用与运算就可以判断该位是否有该信息。

#define FLAGON(a,n) ((a)&(1<<(n)))//判断整数a中第n位是否为1

12.4 或（|）运算

或运算的操作符为|。2个数进行或运算时，就是将这2个数的二进制进行或操作，只要2个数对应的位有一个为1，该位运算结果为1，否则运算结果为0。

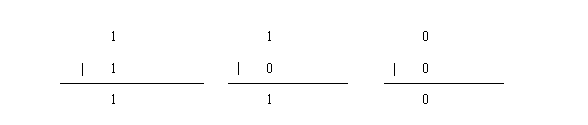
即1|1 = 1，1|0 = 1， 0|0 = 0。那么如何计算两个整数的或运算呢？比如计算15|10，首先15的二进制为：1111，10的二进制为1010，所以15|10为：

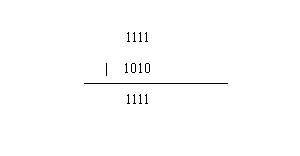
所以15|10=15。

int main(void)
{
    int a = 15;
    int b = 10;
    int c = 15|10;
    printf(“a|b=%d\n”, c);
    return 0;
}

12.5 或（|）运算的应用

或运算性质：任何一个数与1进行或运算为1，与0或运算为本身。可以利用此性质，将某个数的某位置1。

#define SETFLAG(a,n)  ((a) |= (1<<(n)))//把整数a中的第n位置为1

12.6 取反（~）运算

取反运算的操作符为~，为单目运算符。取反运算符顾名思义，就是将一个整数中位为1的变成0，位为0的变成1。

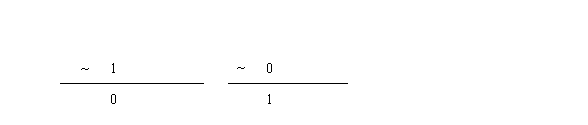
即~1 = 0，~0 = 1。那么如何计算1个整数的取反运算呢？比如计算~10，首先10的二进制为：1010，~10为：

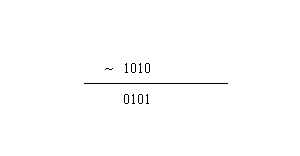
所以~10=5。

int main(void)

{

int a = 10;

int b = ~10;

printf(“~10=%d\n”, b);

return 0;

}

12.7 取反（~）运算的应用

取反运算同与运算结合，可以将一个整数的某位置0，比如：

#define CLEARFLAG(a,n) ((a) &= ~(1<<(n)))//把整数a中第n位置为0

12.8 异或（^）运算

异或运算的操作符为^。2个数进行异或运算时，就是将这2个数的二进制进行异或操作，只要2个数对应的位相同，该位运算结果为0，否则运算结果为1。

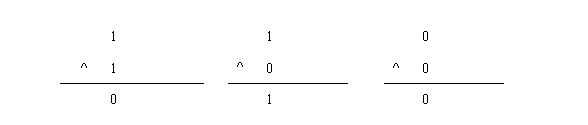
即1^1 = 0，1^0 = 1， 0^0 = 0。那么如何计算两个整数的异或运算呢？比如计算15^10，首先15的二进制为：1111，10的二进制为1010，所以15^10为：

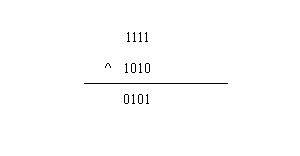
所以15^10=5。

int main(void)
{
    int a = 15;
    int b = 10;
    int c = 15^10;
    printf(“a^b=%d\n”, c);
    return 0;
}

12.9 异或（^）运算的应用

异或运算的性质：

a^a==0
a^0==a

即任何一个数与自身异或为0，与零异或为自身。

1 置零

利用这个性质，可以用于2个数的交换，置零等。

比如，我们在汇编语言里，经常看到这样的汇编语句：

xor eax,eax

这条汇编语句，利用异或性质，将eax置零。

2 交换2个数

异或另一个出名的应用是两个数的交换：

#define SWAP(a,b) \
do{\
    a=a^b;\
    b=a^b;\
    a=a^b;\
}while(0)</p

证明：

假设：a和b的初始值：a=a0,b=b0;

那么：

第一句：a=a^b即a为a0^b0

第二句：b=a^b即(a0^b0)^b0=》a0^(b0^b0)=》a0^0=》a0

第三句：a=a^b即a0^b0^a0=》a0^a0^b0=》0^b0=》b0

因此，通过上面的推导，实现了a与b值的交换。

3 单指针域构造双向链表

此外，异或还可以用在链表中，我们知道，通常的双向链表，需要在链表结点中设置2个指针，指向该结点的前驱和后继结点，但如果使用异或，则可以用单个指针域来表示双向链表：

有任意3个相邻结点：PL， P， PR

那么P->next = PL^PR

对于头结点来说：P没有左边的结点，所以左结点为NULL

所以Head->next = NULL^PR

对于尾结点来说：

尾结点没有右边的结点，所以PR为NULL

Tail->next = PL^NULL

那么在遍历的时候：

按照上述规则生成链表之后，遍历方法如下：

从左往右遍历链表：

pl=NULL;
p=Head;
while(p!=Tail)
{
    pr=pl^(p->next);
    pl=p;
    p=pr;
}

从右往左遍历链表：

pr=NULL;
p=Tail;
while(p!=Head)
{
    pl=pr^(p->next);
    pr=p;
    p=pl;
}

12.10左移（<<）运算

左移运算符为<<。将一个数a向左移动n位记为：a<<n。比如将12向左移动2位如何计算呢？12的二进制为00001100，那么左移动2位为：00110000。无论左移还是右移，都需要用0或者1去填充移动之后空位。在左移的过程中，右边一律用0去填充。左移就没有右移那样分为逻辑右移和算术右移。

比如，将10左移2位，由于10的二进制为：00001010，那么左移2位，右边用零填充的结果为：00101000。

将一个数左移N位相当于将一个数乘以2^N，而将一个数右移N位相当于将这个数除以2^N。

int main(void)
{
    int a = 10;
    int b = a<<2;
    printf(“b=%d\n”, b);
    return 0;
}

上述位运算符的优先级列表如下：

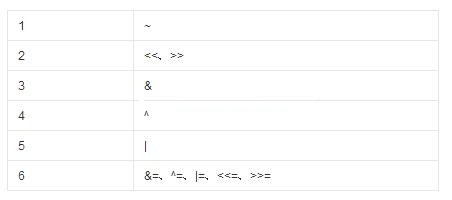
实际上，在讲解运算符的第5章就已经将各个运算符的优先级列了出来。因此，牢牢记住整个运算符的优先级，就没有问题。

12.11 右移（>>）运算

右移运算符为>>。将一个数a向右移动n位记为：a>>n。比如将12向右移动2位如何计算呢？12的二进制为00001100，那么右移动2位为：00000011，即3。

即12>>2为3。

右移动运算分为两种右移，一种为逻辑右移，在移动过程中，左边位用0填充。一种为算术右移，在移动过程中，左边用符号位来填充。

比如对于有符号数：10000011，对于逻辑右移，向右移动3位，那么左边用0填充，变成了：00010000。而对于算术右移，向右移动3位，那么左边用1（1为符号位）填充，变成了11110000。而对于01000011，算术右移3位，那么左边用0（0为符号位）填充，变成了00001000。

在C语言中，右移运算符为算术右移运算符，即左边用符号位来填充。

int main(void)
{
    int a = -3;
    int b = 10;
    int c = a >> 2;
    int d = b >>1;
    printf(“a>>2=%d, b>>1=%d\n”, c, d);
    return 0;
}

12.12 位运算优先级

位运算符的优先级如下图，位置靠前的优先级高于位置靠后的优先级。

而所有的C运算符的优先级与结合律如下图：（从图中可以看出，算术运算符的优先级高于《和》运算符）

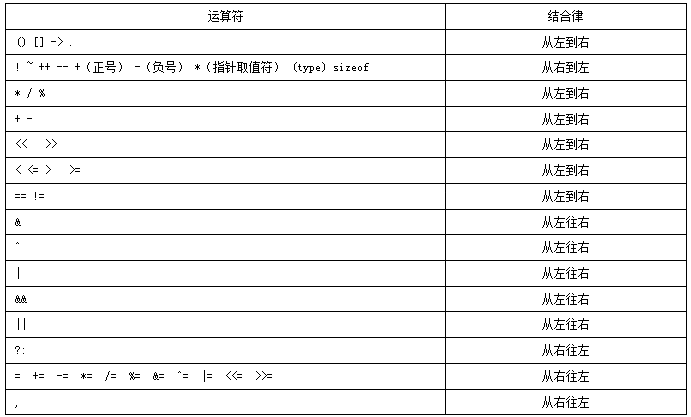
12.13 常见位运算

1．任何一个数和0异或是它的本身：

a^0=a

a^a=0

void swap(int *a, int *b)
{
   
    *a = *a ^ *b;
    *b = *a ^ *b;
    *a = *a ^ *b;
}

1） 将第n位置位或清零：

#define  BITN (1<<n)
置位：a |= BITN;
清零：a &= ~BITN

2） 清除整数a最右边的1。

方法：a & (a – 1)

问题：如何判断判断整数x的二进制中含有多少个1？

分析：此题是微软公司的一道笔试题。下面用&运算来解决此题。

代码如下：

int func(int x )
{
    int countx = 0;
    while ( x )
    {
         countx ++;
         x = x&(x-1);
    }
    return countx;
}

功能	示例	位运算
去掉最后一位	(101101->10110)	x >> 1
在最后加一个0	(101101->1011010)	x << 1
在最后加一个1	(101101->1011011)	(x << 1) + 1
把最后一位变成1	(101100->101101)	x | 1
把最后一位变成0	(101101->101100)	(x | 1) - 1
最后一位取反	(101101->101100)	x ^ 1
把右数第k位变成1	(101001->101101,k=3)	x | (1 << (k - 1))
把右数第k位变成0	(101101->101001,k=3)	x & ~ (1 << (k - 1))
右数第k位取反	(101001->101101,k=3)	x ^ (1 << (k - 1))
取末三位	(1101101->101)	x & 7
取末k位	(1101101->1101,k=5)	x & ((1 << k) - 1)
取右数第k位	(1101101->1,k=4)	x >> (k - 1) & 1
把末k位变成1	(101001->101111,k=4)	x | ((1 << k )- 1)
末k位取反	(101001->100110,k=4)	x ^ ((1 << k) - 1)
去掉整数最右边的1	(100101111->100101110)	x & (x – 1)
把右边连续的1变成0	(100101111->100100000)	x & (x + 1)
把右起第一个0变成1	(100101111->100111111)	x | (x + 1)
把右边连续的0变成1	(11011000->11011111)	x | (x - 1)
去掉右起第一个1的左边	(100101000->1000)	x & (x ^ (x - 1))
取右边连续的1	(100101111->1111)	(x ^ (x + 1)) >> 1

12.14 位运算在软件工程中的运用

在WDK中创建文件的IRP中，有一个Options整数，它的高8位记录了对文件的修改标记。因此可以使用下面的位运算来获取这8位的值：

ulDisposition = (lpIrpStack->Parameters.Create.Options >> 24) & 0xFF;

上面的语句中，先将该整数右移24位，再与0xFF做与运算，即可获得该8位的值。

此外，在实际应用中，会经常使用下面的宏定义来为一个整数设置，清除或者判断某些标志:

#define SETFLAG(a,n)  ((a) |= (1<<(n)))   //把整数a中的第n位置为1
#define CLEARFLAG(a,n) ((a) &= ~(1<<(n))) //把整数a中第n位置为0
#define FLAGON(a,n) ((a)&(1<<(n)))        //判断整数a中第n位是否为1<

在实际的编程过程中，往往会用一个整数的不同位表示不同的数据信息。在访问该整数时，就需要通过位运算来获得或者改变整数的某几位数值。比如在Windows中创建文件时使用的Create数据结构：

struct
{
    PIO_SECURITY_CONTEXT SecurityContext;
    ULONG Options;
    USHORT POINTER_ALIGNMENT FileAttributes;
    USHORT ShareAccess;
    ULONG POINTER_ALIGNMENT EaLength;
    PVOID EaBuffer;
    LARGE_INTEGER AllocationSize;
 } Create;

通常会引用其中的Options如下：

Data->Iopb->Parameters.Create.Options

ULONG Options是一个Windows文件创建过程中的无符号长整数，指示在创建和打开文件时的不同选项。其中高8位指示了CreateDisposition参数（如FILE_OPEN，FILE_CREATE)，低24位指示了CreateOptions参数（如FILE_DELETE_ON_CLOSE)。 为了得到CreateDisposition的值，采取下面的位操作：

(Data->Iopb->Parameters.Create.Options >> 24) & 0x000000ff;

将该整数右移24位，再与0xff做与操作，即可获得CreateDisposition的值。

1．任何一个数和0异或是它的本身，和自身异或为0：

a^0=a
a^a=0

利用上述性质，可以用来计算2个数的交换。

大家应该知道，在计算机里，两个数互相交换，需要定义一个中间的变量来参与交换。如：

int tmp;
int a=10;
int b=20;
tmp=a;
a=b;
b=tmp;

上述代码计算之后，a和b的值完成交换，a的值为20，b的值为10。

如果用异或运算来交换2个数，可以如下方法：

int a=10;
int b=20;
a=a^b;
b=a^b;
a=a^b;

上述运行之后，a和b依然完成了值的交换，但由于是异或位运算，所以效率比上面的代码要高。

证明：

a=10^20
b=a^b=(10^20)^20=10^20^20=10^0=10
a=a^b=10^20^10=10^10^20=0^20=20

把上述代码，可以封装为一个交换2个数的函数如下：

void swap(int *a, int *b)
{
    *a = *a ^ *b;
    *b = *a ^ *b;
    *a = *a ^ *b;
 }

或者用宏来定义：

#define SWAP(a,b) \
do { \
     a = a^b; \
     b = a^b; \
     a = a^b; \
} while(0)

但按照下面的方法来写一个函数，试着将两个数进行交换，是错误的（想想为什么？）

void swap(int a, int b)
{
    a = a ^ b;
    b = a ^ b;
    a = a ^ b;
 }

2.将整数的第n位置位或清零：

#define BITN (1《n)

置位：a |= BITN;

清零：a &= ~BITN

3.清除整数a最右边的1。

方法：a & (a – 1)//该运算将会清除掉整数a二进制中最右边的1。

问题：如何判断判断整数x的二进制中含有多少个1？

分析：此题是微软公司的一道笔试题。下面用&运算来解决此题。 代码如下：

int func(int x )
{
    int countx = 0;
    while ( x )
    {
        countx++;
        x = x&(x-1);
    }
    return countx;
}

4.用异或运算设计一个只有一个指针域的双向链表：

提示：

要实现该设计要求，需要记住链表的头结点和尾结点，并在链表结点的的next域存放前一个结点和后一个结点的异或值。即：

p->next=pl^pr;//头结点的左边结点为NULL，尾结点的右边结点为NULL。

在遍历的时候，从头结点往右遍历的方法：

pl=NULL;
p=Head;
while(p!=Tail)
{
    pr=pl^(p->next);
    pl=p;
    p=pr;
 }

从尾结点往左遍历的方法：

pr=NULL;
p=Tail;
while(p!=Tail)
{
    pl=pr^(p->next);
    pr=p;
    p=pl;
}

5.计算下面表达式的值

(char)(127<<1)+1
(char)(-1>>1)+1
1<<2+3

解答：

(char)(127<<1)+1=(01111111<<1)+1=11111110+1=11111111=-1

(char)(-1>>1)+1=(11111111>>1)+1=11111111+1=0

1<<2+3=1<<(2+3)=1<<5=2^5=32(注意《和+的优先级）

大

中

小

∧

↑

↓

∨