图灵机说明
前言:
话说梦想关于计算机有一天能像人一样思考的科幻作品是一个已经比较古老的主题了。甚至还有人专门设计了的类似“机械人三原则”之类的具体设想,以此来分析将来计算机智能一旦发展到人的智商我们究竟会面临哪些问题。
不过对于另一些科学家来说,往往他们考虑问题的深度可能不够,他们通常更多的是先考虑如何实现某个技术,至于实现该技术后带来的一切社会、政治问题他们都先不作考虑。我想大概研究武器的科学家比较突出吧。总而言之,无论计算机智能高度发展可能带来什么样的危机。能够实现计算机高度拟人化思维的设想永远是计算机研究者的一个梦想。
然而,计算机本身是否具有能像人一样思考的潜力呢?计算机想要模拟人的思考方式究竟要向那些方向发展呢?我在学习了计算机运算原理之后得到了很大的启示。在此跟大家分享一下,好引起激烈争论,活跃论坛气氛。
PS:本人向来拒绝一切用高深词汇和难以理解的专用名词把一个本来容易理解的问题变得难以接受。下面的内容我尽量的用浅显的道理解释。特别是希腊字母我又打不出来,因此涉及专门的数学证明的地方有兴趣的朋友可以参考相关资料。
1,什么是计算机的运算原理(Theory of computation)
所谓运算原理,或者计算原理。就是研究计算机究竟是用什么方法来工作的。通过理解计算机的工作方法,我们可以推断出计算机究竟能做什么和不能做什么。以及用什么方法才能完成某些工作。这就相当于我们研究一下收音机是如何工作的,就能知道收音机能接受什么信号,不能接受什么信号。
计算机科学虽然发展的越来越快,计算机的性能从数字上越来越高。但是仍然有些事情是单靠发展计算机性能无法实现的。就好像你加大收音机的接受频段,也不可能打出一张X光相片一样。
这里需要指出一点,对于有一定编程基础的朋友而言要区分计算机运算原理并不是计算机算法原理。所谓算法,大家都清楚,是用一个类似程序的流程方法把程序表述出来。比如排序算法,你可以选择大数往后排,或者小的数字往前排。然后考虑一下哪种算法在哪种情况下运行效率比较高,哪种算法存储空间效率比较高等等。计算原理完全是另一个概念,它往往不会具体到某一个算法,它可以告诉你计算机“能”或“不能”执行某一种任务。以及一旦要执行一个非常困难的任务,我们应该向哪个方向考虑。这里面更多的是用数学的概念来进行推导和证明。
那么为了研究计算机的运算方法,我们把计算机简化成为几种非常简单的模型。根复杂的计算机系统比,这些模型看起来可以用简陋形容。但是他们对于我们理解计算机的能力却又是必不可少的工具。
计算机的简单模型主要分为三种:有限状态自动机Finite Automaton(FA),下推自动机Push Down Automaton(PDA),以及图灵机Turing machine。这三种模型一个比一个复杂,一个比一个功能更强大。当然这些名词看起来有点玄。我马上用简单的语言给大家解释一下。
2,有限状态自动机(简称FA)
所谓自动机,其实就是不需要人为干预指可以自动执行某个任务的机器。说白了也就是计算机。那么有限状态是指什么呢?就是说这种计算机没有任何动态的存储设备。他不能记录任何数据。因此他的限制很大。
比如说有什么限制呢?他连最简单的数绵羊的任务都执行不了。因为数绵羊随着数字逐渐增加,数字位数逐渐增大,你就需要更多的空间来存储数字。但是因为存储空间有限,数字增大到一定程度必然超过你“有限”的状态。因此他不能执行数绵羊的任务。
需要注意的是,这里有一个可能抬杠的地方,就是大多数程序员都知道计算机的存储空间其实都是有限的,不可能执行一个无限数绵羊的程序。我必须强调一下,所谓有限状态,是指你写好这个程序之后,它就有固定的状态个数了,你无论如何改变计算机性能都无法增加状态的个数。比如说:如果你用高级的方法写一个数绵羊的程序,你现在内存只有1G,当你数到把1G内存都沾满之后就不能继续数了。但是你把内存换成2G就又可以继续数了。但是有限状态的自动机,如果在你程序写好的时候有100个状态,那么你无论增加多少内存,增加多少存储空间,它永远都是100个状态。不会动态的增加和减少。因此我们在这个简化模型中称他的状态“有限”。类似的,以后涉及到有存储空间的其他模型时候,我们都是假设他们的存储空间“无限”,因为他们可用的存储空间能够随着计算机性能的提高而不断的动态增加。
那么FA究竟能执行什么任务呢,他可以执行一些简单的逻辑任务,比如一个控制开门的机器。输入ABCD就开门,其他的输入就不开。那么简化的说就可以设计一个4个状态的自动机,当输入A,就进入状态1,输入B进入状态2,输入C进入状态3,输入D进入接受状态。而在1,2,3任意一个状态里,后面如果跟着的不是我们所期待的密码。比如A后面跟着C,或者AB后面跟着F,这样的错误输入我们就退回到初始状态。(上述例子极为不严谨,仅作理解参考。)这是一个简单的例子,还有一些比较复杂的,比如判断一个二进制数是否可以被11也就是十进制的3整除。这个自动机的构成是下面这个样子的:
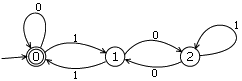
[url=http://www.matrix67.com/blogimage/200812011.gif][/url]
里面有三个状态,A,B,C。其中画了两个圈的状态A是接受状态。另外两个B,C是不接受的中间状态。那么最初始没有输入的时候是0,0除以3自然余0,所以初始时就是接受状态,当输入0的时候始终返回状态A,在输入一个1的时候进入状态B,在状态B时如果输入另一个1的时候返回状态A,以此类推。那么根据这个图,大家可以尝试一下输入二进制数能被3整除的数例如1001(9),10101(21)试试看,看看结果是不是停留在A上。具体原理比较复杂,不详细介绍了。大体意思就是,状态A是所有余数为0的状态,B是所有余数为1的状态,C是所有余数为10(十进制的2)的状态。
那么,要设计一个FA,首先我们要限定一些内容。第一个就是要限定一个输入字符的范围。这个范围可大可小,是人为规定的。比如说如果我们要研究二进制的数学问题,那么自然输入字符就是1和0,研究十进制自然就是0~9,如果研究字母排列问题就是26个英文字母。这个范围规定好了我们才可以讨论自动机的行为,否则像刚才那个判断二进制数是否被某个数整除的问题,如果你输入的是“RH120”自然就超出了可输入字符的范围了。
限定好字符范围之后,就要根据要解决的问题设计出几个需要的状态,几个状态,一般q0表示初始状态,那么在这些个状态中有一个接受状态。也就是只要跳入这个状态,自动机就算接受了这个字符串了,接受状态通常叫做T。(当然根据你定义的任务不同,FA进入接受状态后随着你后续的输入也有可能再次跳出接受状态。)
最后,根据任务的要求,用一个状态之间转换的方式把这些状态连接起来,一个FA就算构成了。这个连接的方法,我们叫它“转换函数”f。其实名字无所谓,大家知道他是状态转换的规律就可以了。
那么根据我们设计的FA,我们既可以规定的字符范围内,按照一定规律组合起来的字符串了。
举个例子,比如我们要设计一个FA,它的字符范围是“a,b,c”三个字符。我们要接受的字符串必须由a,b,c组成。
我们规定凡是由abc组成的字符串中,以ab开头,ba结尾的。我们就接收,其他一概不接受。换句话说,就是ab*****......*****ba这样结构的并且都是由abc三个字符组成的字符串,就是符合这个FA的要求。这个自动机很简单,有兴趣的朋友可以自己画画看。
接下来就是重点中的重点了:1我们给定一个字符范围(简称:字母表),2并且规定字符排列的规律(这个规律我们把它叫做一种“语言”),3如果我们能设计一个FA辨别出符合这个“语言”的所有字符串。————>我们就把这个语言叫做“正则语言”。(反之,写不出一个FA识别这种语言的就叫做“非正则语言”)。
什么样的语言FA没法识别呢?比如:给定字母表{a,b},语言规律是:有n个a,跟着n个b。比如说“aaabbb” "aaaaabbbbb" "ab"就是属于这种语言的。反过来,如果是“abb” “aaab”这样的就不属于这种语言。这种语言就无法用FA识别。为什么呢?因为FA的状态有限,我们无法知道有多少个a后面跟着了多少个b。我们可以写100个状态,有100个a就进入到第100个状态,如果正好有100个b就顺着退回到最初始状态。但是一旦有200个a和200个b,这个FA就无法识别了。而我们的要求却是n个a,跟着n个b。因此面对这类问题,我们需要一个可以动态增长的存储空间。
3,下推自动机(PDA)
好了,我们先复习一下,FA也就是有限状态自动机,他是最简单的计算机模型,他状态有限,他所能接收的“语言”叫做“正则语言”。
那么我们已经知道一个典型的非正则语言,aaaaaa.......(n个a)bbbbbbb........(同样数目的n个b)。用状态有限的FA,是无法识别的。所以我们必须要有一个可以动态增长的存储空间。那么PDA就正好有一个存储空间“堆栈”(stack)。
熟悉计算机的朋友自然知道堆栈是什么东西,可以跳过这部分。我给一些不熟悉的朋友稍微介绍一下。堆栈就是一个存储数据的存储器。他的特点是当你把新的数据存进去的时候。老的数据就被压在下面。如果你想要读取老的数据,就必须把压在他上面的数据删除掉才行。说到这里大家应该明白了吧,就好像枪的弹匣一样,压子弹的时候要以一枚一枚子弹往下压,如果你想要把最后一枚子弹去出来,就必须把上面的子弹都拿掉才行。那么向下压数据的时候,我们就“Push”,向上抽取数据的时候,我们就“pop”。有些人可能问,如果我向一个堆栈依次存储了三个数据,A,B,C,如果我想要读取数据A的话,必须删除掉B,C,岂不是丢失数据了?没错,堆栈就是这样的,如果你要读取压在下面的数据,上面的数据就丢失了,没有其他存储空间给你提供的话你就无法保留那些被“pop”的数据。
PDA就是只有一个堆栈(Stack)的自动机(双堆栈的PDA其实根后面讲的图灵机一样了,这里不作解释,大家不用考虑)。那么上面这个aaaabbbb的语言究竟如何用PDA解决呢?当我们读到一个a,我们就把它push到堆栈里,比如我们读了100个a,我们就push了100个a到堆栈里。当读到b的时候,我们就从堆栈里pop数据,如果是个a我们就读下一个数据,数据还是b就继续pop。当读把最后一个b读完的时候,如果b的个数根a一样,那么数据读到最后一个位置,堆栈里也应该刚好pop空了,这样这串字符就符合我们的语言了。
反过来说,如果读到最后还有b没读完,但是堆栈里却已经空了,就证明b的个数大于a,反过来如果b已经读空了,但是堆栈里仍然可以pop出a来,那b的个数就小于a。这两种情况都是不符合语言要求的。当然为了表明堆栈已经空了,我们可以在push数据前先push一个字母表里未规定的特殊字符比如空格,或者$,#,等。这里是PDA和FA的另一个区别。PDA可以“写”数据,你可以根据自己读到的东西,写入一些数据,甚至为了方便操作可以写入一些字母表里不存在的字符。比如在堆栈push其他数据前,先push一个#,最后等我们pop到最后一个字符‘#’时候,说明堆栈已经空了。
PDA的图比较难懂,因为他本身看起来根堆栈好像没关系,这里就不作介绍了。总之PDA的操作方式就是通过向堆栈里存储数据,以备后面的运算时候使用。
那么相对的FA能识别的语言叫做正则语言,PDA能识别的语言叫做“上下文无关语法”。字面上不太好理解,大家知道就可以了。其实意思就是说PDA的语言里,可以定义一些变量并且可以回环调用自己。(看不懂的朋友可以不用看下面这部分)比如刚才那个语法 n个a跟着n个b。上下文无关语法的不严谨写法就是 S-> a S b|ab意思就是S既可以是a S b,也可以是ab,如果是aaabbb, S就自己调用自己3次, S->a S b, -> a (a S b) b -> a a(ab)b b -> aaabbb。
那么可想而知,凡是FA能识别的正则语言,PDA都能识别,那么还有一些PDA不能识别的呢,就叫做“非上下文无关语法”了,立如把刚才的问题扩展一下,如果字母表是{a、b、c}而字符串规则是n个a,跟着n个b,跟着n个c。例如aaaabbbbcccc或者aabbcc是属于该语言的字符串,很明显一个堆栈push n个a之后,跟随着n个b pop n次,数据全部丢失,后面c的个数就没法比较了。
4,图灵机 (TM)
好了,PDA接受不了的语言自然就要求助更牛B的图灵机了。图灵机跟PDA的区别在于,PDA用的是一个假设无限存储空间的堆栈。而图灵机的存储空间则是一个长条状的无限长度的纸带。用户所输入的字符串完全存留在纸带上。而且如果要进行修改,图灵机可以在纸带上写入数据。为了读取或改写纸带上某个位置,图灵机有一个指针,可以在纸带上左右移动,指到什么位置,就读取或改写这个位置。根PDA一样,为了方便操作,图灵机可以写入字母表未规定的特殊字符。那么图灵机如果解决上面那个问题。
假设输入的字串是 $ aaaabbbbcccc $ , “$”符号表示开头和结尾,
图灵机指针读到第一个a把它改写成#,然后忽略后面所有的a一直读到b。字符串变成$#aaabbbbcccc$。
第一个b也改成#,并忽略接下来的b直到读到c,字符串变成$#aaa#bbbcccc$。
同样第一个c改成#,并忽略所有c读到末尾$。字符串变成$#aaa#bbb#ccc$。
然后返回头去重复上面操作,字符串变化如下,“^”符号为指针位置
$##aa #bbb #ccc$。
^
$##aa ##bb #ccc$。
^
$##aa ##bb ##cc$。
^
$###a ##bb ##cc$。
^
$###a ###b ##cc$。
^
$###a ###b ###c$。
^
$#### ###b ###c$。
^
$######## ###c$。
^
$######## ####$。
^
当所有字符都改成#时候,字符串符合语言,接受。如果改完所有字符串仍然有字母残留,说明该字母数量多于另外的字母,则字符串不符合语法被拒绝。
通过读取和改写纸带上的数据,图灵机可以实现PDA和FA无法实现的任务。前面我提过一点,双堆栈PDA其实根图灵机一样,大体原理就是你吧一个堆栈的东西推到另一个堆栈里,当你需要向另一个方向读取的时候就把他反方向退回来。这就像图灵机指针左右读取纸带上的数据一样。
但是图灵机也有双纸带甚至多纸带的图灵机。虽然如此,多纸带图灵机的功能并没有超过单纸带的图灵机。多个纸带只需要全写在一个纸带上,并用特殊字符将不同纸带内容区分开。这样单纸带的图灵机完全可以执行多纸带图灵机的任务。因此虽然有些时候为了研究方便,我们会用到多纸带图灵机。但是一定要明确不论纸带有多少,图灵机的功能都没有提升。
那么图灵机究竟厉害在哪里呢?就厉害在他不但可以执行一个PDA或FA的任务,它还可以自己执行自己的任务。这就叫做通用图灵机。通用图灵机的意思就是,它首先把另一个图灵机M的运算法则和转换状态都写在纸带上,然后把M要进行运算和判断的字符串写在另外一个纸带上。然后按照M的规则,M运行一步,他就在纸带上操作一步。最终通用图灵机的运行结果跟M的运行结果完全一样。也就是说通用图灵机的定义就是,如果我给定一个自动机M(包括FA, DFA, TM),和给他输入的字符串叫S,那么把这个自动机和他要运算的字符串编写到一个纸带上<M,S>然后交给通用图灵机UM执行。其结果将和S在M上的执行结果一致。
5,图灵机不能解决的问题
那么我们已经介绍了计算机简化的三种模型,其中最高级的,也就是现代计算机能够完成的任务,它也都能完成的,就是图灵机。但是图灵机也有完成不了的东西。这就到了一个很主要的问题“停机问题”。
首先,图灵机本身并不一定会停止,图灵机对一串字符的运算结果有三种1,接受。2,拒绝。3,无限循环或因为无运算规则而崩溃。其中,2、3两种情况都属于不接受情况。那么现在问题来了。我们可不可能写一个通用图灵机,UM,让他以任意另外一个图灵机M和它的输入字符串S组成纸带信息<M,S>。让UM判断M运行S的时候,是否会陷入无限循环中。如果会无限循环,则接受<M,S>,如果不会则不接受?注意,M不是某一个指定的图灵机,而是任意的一个图灵机,也就是说白了,你可不可以写一个程序,让他判断任意一个其他的程序,是否会陷入无限循环。
答案是否定的,证明的方法有很多种,包括一个最经典的哲学方法“一个理发师,他为所有那些不给自己理发的人理发”,“这个理发师的头发谁来理?”。
如果图灵机UM可以判断任意图灵机M以任意字符串S的输入是否陷入无限循环。那么以UM自己和另一个字符串为输入,让UM判断自己会不会陷入无限循环呢?问题是如果UM会陷入无限循环,那么UM自己就无法停机。他就无法给出最终结果。反过来如果UM能够停机,那么他就并没有因为UM自己的输入陷入无限循环。
因此,不存在一个图灵机,能够判断所有其他的图灵机针对所有的输入字串是否停机。
停机问题仅仅是图灵机的一个经典问题。停机问题本身的证明不是用这种哲学方法证明的,数学证明法有几种,因为比较复杂就不在此介绍了。另外还有很多图灵机不能解决的问题根据“复杂性”(就是如果一个问题A能解决,问题B就可以解决,说明B比A简单,已知B无解,因此A也无解之类)理论可以相互推导。
那么身为程序员的我们是否能解决停机问题呢?幸运的就是我们是可以解决停机问题的,人脑的运算方法可以发现各种陷入无限循环的逻辑情况,虽然有些时候非常复杂,但是通过一段时间的分析仍然可以判断一个程序是否会在某个输入情况下陷入无限循环。
6,计算机的“智商”与冯•诺伊曼结构。
经过以上的一段论述,很可能有人会认为我们最终会落下一个否定的结论。“计算机永远不可能像人一样思考”。比较主观的说,虽然我没有什么确实的证据,但是我却并不认同这个结论。我只是认为大家应该走出一个误区。
我们长久以来一直认为计算机技术的发展方向其实并非是影响计算机“智商”的因素。的确,我们的计算机运算速度越来越快,我们的计算机存储空间越来越大。我们能用计算机引擎写出更漂亮的3D引擎和更逼真的物理引擎。但是这些都没有从本质上解决以前计算机所不能解决的“难题”。老式计算机也可以执行复杂的3D运算,只不过他们执行的慢一点,或者说好吧我承认他们慢很多,但还不是无法执行。可是无论是最新的intel i7还是老式的8086都无法解决图灵机的“停机问题”。原因何在呢?因为我们的计算机使用的是“冯•诺伊曼结构”也就是说我们的计算机根本就是一个投入实用的通用图灵机。他的运行方法就是把另外一个图灵机(软件程序)存储到纸带(内存)里然后按照这个软件图灵机的步骤一步步执行并得出结果。因此无论计算机的性能如何提升,他都没有从本质上,没有从计算能力上提升计算机水平。
要想提高计算机的智商,需要新的结构,也就是说,需要一种比FA、PDA、和图灵机都更高级的结构,凡是图灵机不能判断的问题,他都可以判断。要建立这种新结构,很可能我们要直接剖析我们自己大脑的结构来建立运算模型。这样我们的问题可就不再是计算机能否像人一样思考了,而是我们能否彻底认识自己的大脑。不过我相信,即使我们不能完全模拟出人脑,但是因为脑的结构是固定且客观存在的,因此通过解析脑的结构,即使不能彻底理解脑的全部工作方式,起码可以建立一个新的计算模型。从而从本质上提高计算机的“智商”。
希望大红能尽早建立一个新的计算机体系,从此以后图灵奖改叫“Redass奖”可喜可贺可喜可贺。